[전자기학] 전계, 전기장 (Electric Field) 의 뜻.

전자기학을 배우면서 가장 먼저 만나는 것이 전기장(또는 전계 = Electric Field)이다.  전기장을 이해하기 어려운 가장 큰 이유는 장(場, Field)의 개념을 이해하기가 쉽지 않기 때문이다.

물리학을 처음 배울 때 물체에 힘을 직접적인 접촉에 의해 가하는것으로 배운다. 이해하기가 쉽기 때문이다. 그러다가 전자기학부분에서 장의 개념을 배우게 되는데 이 과정에서 중간단계의 설명이 없기 때문에 이해하기가 어렵다. 공간을 통해서 힘을 전달한다고 하는데 어떻게 된 일인가. 직접 만져보지도 않았는데도 뭔가가 느껴지는 현상에 대해서 알아보는 것은 재미있는 일이다.

시간에 따라서 전하분포가 변하지 않는 정전계(Electrostatic Field)를 대상으로 한다.

1. 기(氣, Force) 에 대한 생각

우선 기(氣)에 대해서 생각해 본다. 전기(電氣) 라는 말에 기(氣)가 포함되어 있다는 사실을 주목해 볼 필요가 있다. 일상 생활에서 기(氣)라는 표현을 다양하게 쓰고 있다. 미녀가 나타나면 분위기(雰圍氣)가 달라진다는 표현을 한다. 우리가 모르는 사이에 기(氣)가 달라진다고 표현을 흔하게 쓰고 있는 것이다. 

마음에 드는 여자애가 옆자리에 앉는다면 수업에 집중이 될까. 뭐가 변한 것일까.

(1), (2) 를 비교해 보자. 차이점은 뭘까. 한쪽은 공허한 공간이고 다른 한쪽은 미인이 있다. 그 둘을 바라보면서 뭔가가 달라졌다는 느낌이 들지 않는가.

(1), (2) 를 다시 그려보면 다음과 같다. 뭔가 변했다는 느낌을 갖도록 하기 위해서 공간이 변한 것처럼 그렸다.

(2) 를 보면서 '빠져들어간다'는 느낌이 들지 않는가.
 

생각해보면 신기하다. 분위기가 변하고 빠져들어간다는 말을 흔하게 쓰고 있다. 이런 느낌으로 접근하면 장(Field)의 개념을 이해하기가 더 편해질것 같다.

아인슈타인은 공간이 절대적인 것이 아니라고 말했다. 실제로 중력에 의해 지구 주변의 공간이 변하는 것을 다음과 같이 표현한다.

그걸 생각해보면 미인에 의한 공간의 변형이라는 상상력을 발휘해 보는 것도 좋을 것 같다.

2. 에너지와 물질

에너지와 물질의 관계를 보면 사실상 거기에서 거기다. 물질이 에너지가 되고 에너지가 물질이 된다. 원자력발전소에서는 물질을 에너지로 만들고 입자가속기에서는 에너지를 물질로 만든다.

물질에서 에너지로 다시 물질로

이러한 관점에서 물질은 에너지가 집중된 형태라는 표현을 쓰기도 한다. 물질이 에너지가 집중된 형태라면 물질이 아닌 공간에도 에너지가 넓게 퍼져 있어야 할 것이다. 그럼 공간은 비어있는 것이 아니라 뭔가가 채워져 있는 것으로 이해할 수 있다. 그런식이라면 물질이 이동하면 공간도 변한다는 개념이 어느정도 이해가 된다.

물을 생각해 보자. 잔잔한 호수이든 매서운 파도이든 물이라는 사실에는 변함이 없다. 파도와 물은 별개가 아니다. 파도는 물질이고 그 주변 공간은 비어있다고 생각하면 곤란하다. 파도와 그 주변 공간(Field)은 비어있는 것이 아니며 다만, 파도가 에너지가 높은 상태이기 때문에 눈에 잘보이는(관측되는) 것일 뿐이다.

파도와 물을 구별할 수 있을까?

달라진 것은 에너지 분포가 달라졌다는 것이다. 에너지가 달라졌다는 것을 공간이 변형되었다고 생각해 볼 수도 있다. 그래서 전자기학 책에서 전기장(Electric Field)을 설명할 때 공간에 에너지를 저장한다는 표현을 쓰기도 한다. 개인적인 선호도 차이겠지만 에너지 분포가 달라졌다는 표현보다 공간이 변형되었다는 표현이 더 마음에 든다. 눈으로 쉽게 보면서 이해할 수 있기 때문이다.

세상을 어떻게 바라볼 것인가 하는 것은 관찰자가 무엇을 보고자 하느냐에 따라 달라진다.

땅부자 왈, 나는 노른자와 흰자만 생각한다.

현실을  객관적으로 그리고 있는 그대로 별다른 의미를 두지 않고 관찰하는 방법도 있겠지만, 특별한 목적을 가지고 바라본다면 좀 더 단순 명쾌하게 결론을 내릴 수도 있다. 내가 보고자 하는 것 이외의 것은 부차적인 것으로 관찰 목적에는 크게 영향을 주지 않는다.

정전기학에서는 (1)전기적 성질을 가진 입자들이 분포한 모양과 (2)그 입자들이 서로에게 가하는 힘 만 생각한다. 이것이 정전기학에서 바라보는 세상의 모습이다.

 

3. Force

영화 스타워즈에서는 Force 에 대한 이야기가 많이 나온다. 그런데 이 Force 라는 것은 기(氣) 에 가깝다. Force 가 느껴진다는 말은 기(氣)가 느껴진다는 말과 같다. Darth Vader 가 주변에 다가온다면 어떨까. 감히 접근할 엄두조차도 내기 어려울 것이다. 이런 느낌을 다음 그림처럼 상상해 보자.

위로 솟은 공간을 아래에 등고선으로 평면에 표시했다.

그럼 위의 미인이 등장하는 공간을 다시 등고선으로 표시해 볼 수 있다.

그런데, 이제 문제가 되는 것은 미인이 등장함으로서 변형된 공간의 정도를 측정하는것이다. 측정을 해보려면 '느껴'보면 된다. 그런데 같은 미인이라고 할지라도 사람마다 '느껴지는'정도가 다르다. 정말 급한 사람은 치마만 둘러도 민감하게 반응할 것이고 관심이 없는 사람은 별 느낌이 들지 않을 것이다. 이런식으로는 미인이 공간을 어떻게 변형시켰는지 알아보기가 어렵다.

그럼 객관적인 방법을 생각해 보자.

가장 작은 단위를 사용하면 된다. 여기서는 매력을 나타내는 Charm 을 단위로 생각해 보자. 남자의 매력을 +Charm 이라고 하고 기본단위를 +1C 으로 정한다. 그리고 미인에 의해 변형된 공간에 기본단위 +1C 을 가진 남자를 놓아본다. 그 때 남자가 느끼는 정도를 측정해 보면 객관적인 힘의 크기를 알 수 있을 것이다. 이 때의 단위를 N/C 이라고 정한다. +1C 이 느끼는 힘의 세기라는 뜻이다.

한가지 주의해야 할것은 실제로 +1C을 놓은 것이 아니라는 것이다. 변형된 공간에 '만약' +1C을 놓는다면 그렇게 '느껴질'것이라는 것이다. 즉, +1C을 놓았을 경우 그렇게 느껴질 것이라는 것을 예상해 볼 수 있다는 것이다. 이것은 앞으로 남자가 주변 공간에 다가온다면 영향을 미칠수 있는 잠재능력을 나타내는 것이다. 그리고 그 때 느껴지는 정도를 N/C 으로 표시한 것이다. 그림에서 점선으로 표시한 것은 이런 이유 때문이다.

+1C 은 꽤 큰 값이며 만약 실제로 +1C 의 전하가 공간상에 위치한다면 주변공간에 상당한 영향을 미치게 된다. 그렇기 때문에 원래의 전기적 공간이 아닌 +1C 에 의해서 변형된 공간을 측정하게 되는 것이다. 이런 논리적인 모순점에 대해서 전자기학 책에서는 다음과 같이 설명하고 있다.

Fundamentals of Engineering Electromagnetics / David K. Cheng 에서는

"The test charge q, of course, cannot be zero in practice; as a matter of fact, it cannot be less than the charge on an electron. However, the finiteness of the test charge would not make the measured E differ appreciably from its calculated value if the test charge is small enough not to disturb the charge distribution of the source."

"물론 시험전하 q는 실질적으로 0이 될수는 없다. 실제로는 전자의 전하량보다 적을수는 없다. 그러나 시험전하의 전하량이 충분히 적어서 원천전하의 전하분포에 영향을 주지 않는다면 시험전하의 유한성(0이 아니라 값이 있는)이 전기장의 측정값과 계산값을 현저히 다르게 만들지는 않을 것이다."

Fundamentals of Physics / Halliday , Resnick , Walker 에서는

"Although we use a positive test charge to define the electric field of a charged object, that field exists independently of the test charge."

"비록 우리가 대전된 물체의 전기장을 정의하기 위해서 양의 시험전하를 사용하기는 하지만, 전기장은 시험전하와는 독립적으로 존재한다."

시험전하라는 개념은 전기장의 정의를 위해서 도입한 것이지만 원천전하에는 영향을 주지 않는 (최소한 거의 주지 않는다고 보는) 개념적인 전하라고 보면 될 것이다. 그런데 전기장을 계산하라고 하면 시험전하가 개념적으로라도 있어야 하므로 (시험전하가 없더라도 전기장은 존재하겠지만) 두개의 전하가 필요한 것이다. 

전기력(Electric Force)의 경우는 C 를 Coulomb 이라고 생각하면 된다.

전하를 가진 입자들 사이에 작용하는 힘을 전기력(Electric Force)이라고 하며,

\( \vec{F} = q\vec{E}\) 라고 표시한다. 원래는 쿨롱이 연구한 것에서 시작한 것이지만 약간 변형된 형태로 발전했다.

전하들 간에 작용하는 힘을 직접적으로 표현하는 대신, 전하들이 만들어낸 전기적 공간(Electric Field)을 먼저 표시한뒤에 나를 그 공간에 놓았을 때 가지는 느낌을 표현하는 방법으로 발전했다. (나는 q이며, 그녀는 Q이다. Q가 만들어낸 공간에 나, q가 위치한 것이다.) 즉, 내가 거기 있기 전에도 그 공간은 존재했던 것이지만 내가 거기 있음으로 해서 [느낌]이 생기는 것이다. 미모의 여성들이 있는 공간에 내가 들어선다면 나는 알듯 모를듯한 미묘한 [느낌]을 가지게 된다. 그 공간은 내가 들어서기 전에도 존재했던 것이며 내가 아닌 다른 이가 들어가도 [느낌]이 생기는 공간인 것이다. 그럼, 그 공간은 무엇인가를 느낄 수 있도록 하는 잠재력(potential)이 있는 공간이라고 할 수 있을 것이다.

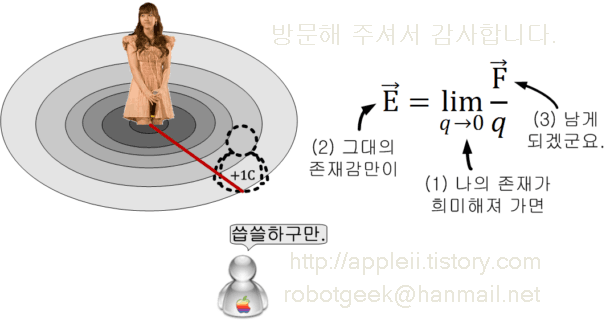
문제는 내가 그 공간에 들어서면, 나에 의해서도 공간이 변형된다는 점이다. 서로의 상호작용에 의해서 작용하는 것이 전기력의 특징이다. 때문에 어느 일방이 존재하는 것만으로는 전기력이 작용하지 않는다. 하지만, 그럼에도 어느 한쪽의 잠재력만을 평가하기 위해서는 [나]라는 존재는 희석되어 있는듯 없는듯 해질 필요가 있다. 전하에는 최소 단위가 존재하므로(전자 1개, 양성자 1개가 최소단위) 더 이상 작아질수는 없다. 실제로는 일어날 수 없는 일이지만 원래의 Source 에 미치는 영향이 거의 없을 만큼 충분히 작다면 Source 가 만들어낸 전계는 Source 의 잠재력으로 평가할 수 있다. (그러나, 완전히 0은 아니다. 무인도에 미인 혼자 있어봐야 성적 매력 따위 논할 가치도 없다.)

전하가 하나가 아니라 여러개라면 어떻게 될까? 각각의 전하들이 주변 공간을 변형시킬 것이다. 양전하라면 솟아오른 모양으로, 음전하라면 아래로 내려간 모양으로 나타날 것이다. (시험전하를 +1C 으로 가정했을 경우이다.)

결국, 전하들의 분포는 전기적 공간의 지형도를 만들어낸다고 할 수 있다. 이렇게 생각하면 전기적 위치에너지 (Electric Potential)를 이해하는 것이 더 쉬워진다. 양전하는 산을 만들고 음전하는 골을 만든다. 산을 오르려면 에너지를 소모해야 한다. 그리고 그 에너지는 해당 지점의 위치에너지로 변환된다.

위의 그림에서 전하가 위 아래로 움직이면 어떻게 될까. 격자가 있는 면을 수면(the surface of the water)이라고 생각해 보면 쉽게 상상이 된다. 파도(wave)가 발생할 것이다. 물이 출렁이면 water wave 이고, 전하가 출렁이면 radio wave (전파) 가 된다.

불교에서 사용하는 표현중에서 색즉시공(色卽是空), 공즉시색(空卽是色) 이라는 말이 있다. 그 해석에 대해서는 여러가지가 있을 수 있겠지만 (대부분 쓰잘데기 없는 해석임) 그나마 양호한 해석은 http://k.daum.net/qna/view.html?qid=3iFsy 에서 '오로지팔정도' 의 해석이다. 물질과 에너지의 관계에 대해서 '아주 그럴듯하게' 설명하고 있다. 과학이란 어짜피 말장난일 뿐이므로 '그럴듯한' 해석이 가능하다면 그걸로 충분하다.

색(色)은 빛이고 공(空)은 물질이다. 빛은 에너지라고 말할 수 있으므로 '에너지는 곧 물질이고, 물질은 곧 에너지이다.' 라는 해석이 가능하다. 실제로 중력장이나 전기장을 설명할 때 백열전구가 빛을 내는 그림을 자주 예로 든다. 그리고 면적법칙에 의해서 거리가 멀어질수록 그 영향력은 제곱에 반비례한다고 설명한다. 중력을 만들어내는 질량이나 전기력을 만들어내는 전하 모두 물질이라고 하지만 실제 설명은 빛(에너지)를 통해서 설명하고 있다. 설명의 편의성을 위해서 백열전구가 내는 빛을 예로 든 것이겠지만 '에너지는 곧 물질이고, 물질은 곧 에너지이다.' 라는 해석과도 '그럴듯하게' 맞아 떨어진다.

전자기학을 배우는데 이런 골때리는 해석까지 해야 되는 이유는 '그럴듯해야' 자연스럽게 받아들일 수 있기 때문이다. [가우스 법칙과 전속밀도] , [전기적 위치에너지] 를 이해하는것이 얼마나 어려운 일인가. 계산하는 것은 어렵지 않으나 왜 그렇게 계산해야 하는지는 받아들이기 어렵다. 교과서를 쓰는 사람들이 '과학적이지 않기 때문에' 라는 이유 때문에 별도의 해석을 하지 않는 모양이지만, 과학이란 말장난일 뿐이라는게 나의 생각이다. 볼츠만(Boltzman)과 마흐(Mach)의 논쟁을 보면 그런 생각이 더 확고해진다.

"기체분자운동론이라니... 뭐 이런, 골때리는 생각이 다 있나." 

고등학교 물리교과서에는 별다른 설명이 없지만 기체분자운동론을 주장한 볼츠만은 사람들의 비웃음을 견디다 못해 자살을 했다. 소심과 우유부단 덩어리인(거기다 허영심까지 있는) 볼츠만으로서는 남들이 인정해주지 않는 현실을 받아들이기 어려웠던 것이다. 기체분자운동론을 처음 접하고 '이런 캐병신같은 생각을 한 놈이 누구야?' 라고 생각하는 것이 당연한 것이다. 한 사람을 죽음으로 몰아갈 정도로 사람들에게 받아들이기 어려운 생각이기 때문이다. 

열받은 물체가 일을 하는 원리는 조그맣고 깜찍하고 올망졸망한 것들이 벽을 두드리는 것이라고 말하는 모습을 상상해 보라. 원자가 실재하는지 아닌지는 알 수 없다. 다만, 고 깜찍한 것들이 치맛자락 휘날리며 움직일 때는 주변이 후끈후끈해진다는 해석은 충분히 받아들여질 수 있을 것이다.

과학은 어짜피 말장난일 뿐이라는 것을 인정하고 조금 더 느슨하게 생각하면 받아들이기는 더 쉬운것 같다.

전기장은 N/C 으로 표시하는 것이 원래의 의미에 맞지만 실제로는 V/m 단위를 더 많이 쓴다. 전압이 더 익숙한 단위이기 때문이다. 전압을 중심으로 표기할 경우 회로의 관점에서 이해하기가 더 쉬워진다. 이런저런 제한조건을 주면 간단한 회로는 전자기학의 관점이 아닌 회로이론의 관점으로 볼 수 있다.

이후로는 N/C 대신 V/m 로 전기장의 세기를 표시하기로 한다.

전기장을 구하는 구체적인 방법은 다음과 같다. 

(1) 점전하가 원점에 있는 경우 (Point Charge at the origin)

중심에 전하(Electric Charge)가 있고 주변에 균일하게 전기력이 영향을 주는 경우, 가우스 법칙(Gauss's Law)을 이용하여 전속(Electric Flux)을 구할 수 있다. 전속을 모두 합하면 가우스 면(Gaussian Surface)내부의 전하를 구할 수 있다. 가우스 면을 구(Sphere)형태로 잡으면 적분의 결과가 구의 표면적이 된다.
\(Q = 4\pi R^2 D_R = 4\pi R^2 (\epsilon E_R) \)
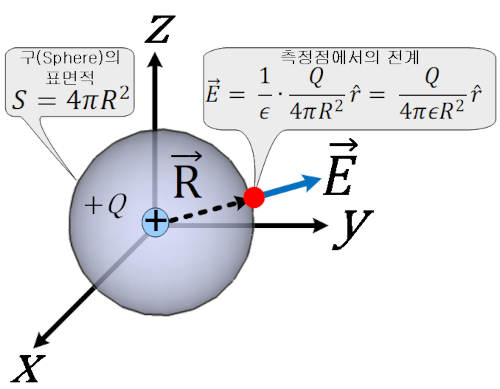
이것을 D_R  과 E_R  에 대해서 정리하면,  \( D_R = \epsilon E_R \text{ } , \text{ } E_R = \frac{1}{\epsilon}D_R \) 이므로
\( D_R = \frac{Q}{4\pi R^2} \text{ } , \text{ } E_R = \frac{1}{\epsilon} \cdotp \frac{Q}{4\pi R^2} \)
이때 전기장은 \( \vec{E} = E_R \hat{R}\) 이므로 다시 정리하면
\( \vec{E} = \frac{1}{\epsilon}\cdotp \frac{Q}{4\pi R^2} \hat{R} = \frac{Q}{4\pi \epsilon R^2} \hat{R} \text{ } \) (V/m)

위의 수식을 주의깊게 볼 필요가 있다. 수식이 전개되는 흐름을 잘 이어나가지 못하면, 4πε 이 왜 나오는지 이해하지 못하게 된다.
\( k = \frac{1}{4\pi \epsilon} \text{ } , \text{ } \vec{E} = k\frac{Q}{R^2} \hat{R} \)4πε 을 묶어서 상수 k 로 쓰는 경우도 있는데 이 단계까지 가면 완전히 미궁에 빠진다. 모양을 예쁘게 만드는것이 중요한 것이 아니라 그 뜻이 무엇인지 아는것이 더 중요하다. 다소 지저분한 모양이더라도 의미가 명확하게 드러나는 식이 이해하기에는 더 좋다.

전기장 \(\vec{E} \) 를 설명하는데 난데없이 \(\vec{D} \) 가 등장하는 것이 꽤 당황스러울 수 있다. 보통 전기장은 교과서의 처음에 등장하며, 유전체는 물질내에서의 전기장 부분에서 다루기 때문이다. 그러나 \(\vec{E} \) 를 이해하기 위해서는 \( \vec{D}\) 를 이해할 수 있어야 한다. 이렇게 되면 유전체를 먼저 공부해야 하는건지 전계를 먼저 공부해야 하는 건지 알수가 없어 어려움이 따른다. 아마도, 전자기학 연구의 역사를 거슬러 올라가다 보면 나중에 발견된 사실에 의해 이전에 설명되었던 원리를 재해석하는 과정이 있었던 듯하다. 그런 과정을 거치면서 내용이 뒤죽박죽 되어버린것 같다. 어찌되었건  \( \vec{E} = \frac{Q}{4\pi \epsilon R^2 } \hat{R} \) 속에는 점대신 면을 중심으로 이론을 전개시키고 공간은 기본적으로 유전체라는 사고방식이 깔려있다는 점을 이해하면 된다.

교과서마다 수식의 표기방법이 제각각이고 , 심지어는 같은 교과서 내에서도 표기방법이 달라지는 경우가 많다. 하지만 보통의 경우 전하가 있는 곳에서 측정점까지의 거리는 R 로 표시한다. r로 표시하는 경우도 있으나 전하가 좌표계의 중심에 있는 경우일 때 뿐이다. 중심에 있지 않은 경우에는 R로 표시해야 하는데 , 따로따로 생각하면 귀찮기 때문에 전하가 중심에 있는 경우에도 R로 표시하기로 한다. (개인적으로는 표기방법에 일관성이 있는 것은 Cheng 책 인것 같다.)

마찬가지로 전하량을 Q 또는 q 로 표시하는 경우가 있는데, 가우스 적분을 해서 그 표면 내부에 있는 전하량의 총합을 Q로 하기로 한다. (전하가 하나뿐인 경우에는 Q = q 이다.) 전하가 여러개 있을 경우 구별하기 위해서 q 로 표시한다.

(2) 점전하가 원점에 있지 않은 경우 (Point charge not at the origin)

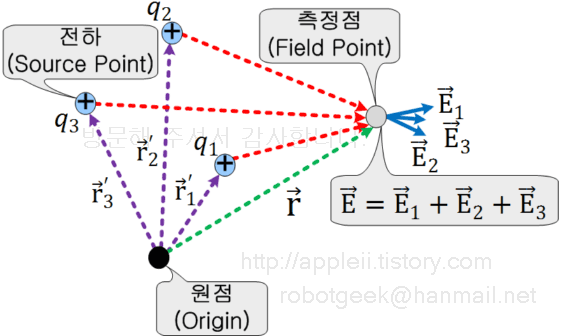
일반적으로 전하가 위치한 곳(Source Point)과 측정하려는 곳(Field Point)을 각각 r' 과 r 로 해서 다음과 같이 표시한다.

\( \vec{E} = (\frac{1}{\epsilon} \cdotp \frac{Q}{4 \pi R^2})\hat{R} = \frac{Q}{4 \pi \epsilon R^2}\hat{R} = \frac{Q}{4 \pi \epsilon R^2}\cdotp \frac{\vec{R}}{R} \)
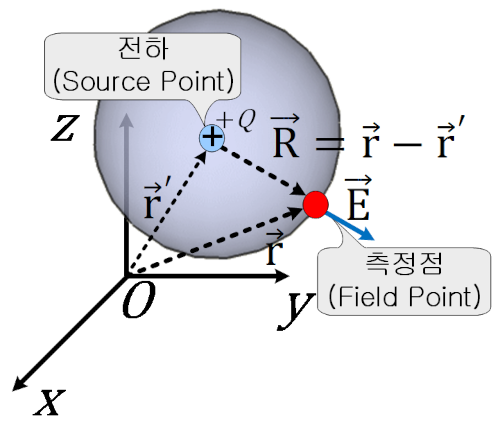
\( = \frac{Q}{4 \pi \epsilon R^3} \vec{R} = \frac{Q}{4 \pi \epsilon} \cdotp \frac{\vec{r} - {\vec{r}}' }{| \vec{r} - {\vec{r}}' |^3} \) (V/m)

(3) 점전하가 여러개 있는 경우

만약 점전하가 여러개일 경우는 중첩의 원리(principle of superposition)를 이용하여 각각의 전하에 의해 측정점에 미치는 전계를 구한 후 모두 합한다. 

\( \vec{E} = \frac{1}{4 \pi \epsilon} \sum\limits_{k=1}^n q_k \frac{\vec{r}-\vec{r}'_k} {|\vec{r}-\vec{r}'_k |^3} \) (V/m)

자유공간에서 전하량 -12nC 와 24nC 인 점전하가 직각좌표계에서 각각 점 (-4, -1, 7) 과 점 (6, -5, -1)에 놓여 있을 때, 점 (-2, 3, 3) 에서 전계를 구하라. 단, 여기서 거리를 나타내는 단위는 미터이다.

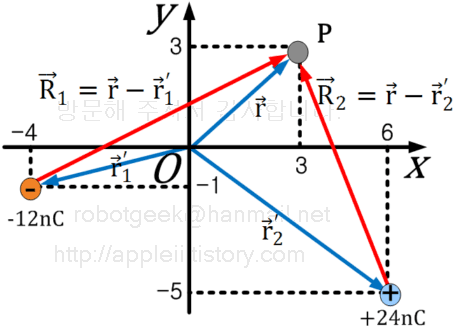
 z축은 생략하고 x, y 축만을 그리면 위와 같다. 

\( \vec{r}'_1 = -4\hat{x} - \hat{y} + 7\hat{z} \)
\( \vec{r}'_2 = 6\hat{x} - 5\hat{y} -\hat{z} \)
\( \vec{r} = -2\hat{x} + 3\hat{y} + 3\hat{z} \)
\( \vec{R}_1 = \vec{r} - \vec{r}'_1 = 2\hat{x} + 4\hat{y} - 4\hat{z} \)
\( \vec{R}_2 = \vec{r} - \vec{r}'_2 = -8\hat{x} + 8\hat{y} + 4\hat{z} \)
\( \vec{E} = \frac{1}{4 \pi \epsilon} \sum\limits_{k=1}^n q_k \frac{\vec{r}-\vec{r}'_k} {|\vec{r}-\vec{r}'_k |^3} \) (V/m) 이므로 점 P에서의 전계는

\( \displaylines{ \vec{E}_P = \frac{1}{4\pi \cdotp \left(\frac{1}{36\pi}\times 10^{-9}\right)}\cdotp \\ \left\{ (-12 \times 10^{-9}) \cdotp \frac{2\hat{x} + 4\hat{y} -4\hat{z}} { \left( \sqrt{2^2 + 4^2 + (-4)^2 } \right)^3 } \\ + (24 \times 10^{-9}) \cdotp \frac{-8\hat{x} + 8\hat{y} + 4\hat{z} }{\left(\sqrt{(-8)^2 + 8^2 +4^2 }\right)^3} \right\} \\ = (-\hat{x} -2\hat{y} + 2\hat{z}) + (-\hat{x} + \hat{y} + 0.5\hat{z} ) \\ = -2\hat{x} -\hat{y} +2.5\hat{z} \text{ } (V/m) } \)
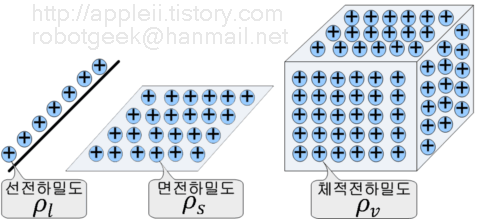
(4) 선전하, 면전하, 체적전하의 경우

선전하, 면전하, 체적전하에 대한 적분은 다음과 같다.

\( \displaylines{ \vec{E} = \frac{1}{4\pi \epsilon}\int_L \frac{\vec{r} - \vec{r}' }{|\vec{r} - \vec{r}'|^3 }\rho_l dl' \text{ } (V/m)\\ \vec{E} = \frac{1}{4\pi \epsilon}\int_S \frac{\vec{r} - \vec{r}' }{|\vec{r} - \vec{r}'|^3 }\rho_s ds'\text{ }(V/m) \\ \vec{E} = \frac{1}{4\pi \epsilon}\int_V \frac{\vec{r} - \vec{r}' }{|\vec{r} - \vec{r}'|^3 }\rho_v dv'\text{ }(V/m) } \)

직선이고 무한한 선전하가 균일한 전하밀도 ρ_l (C/m) 로 공기중 (ε = ε₀)에서 다음과 같이 놓여 있을 때  전계를 구하라.

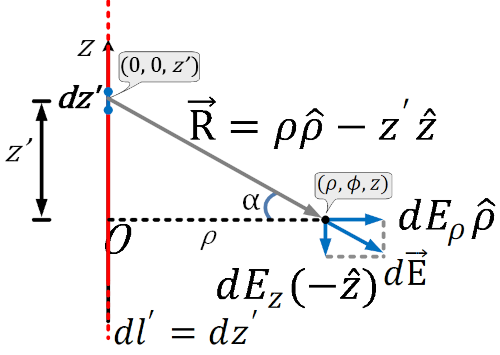
무한 선전하의 경우 적당한 좌표계는 원통좌표계이다. 원통좌표계를 이용하여 Source Point 에서 Field Point 에 이르는 벡터와 미소전하를 구하면 다음과 같다.\( \vec{R} = \rho\hat{\rho} - z'\hat{z} \text{ } , \text{ } dl' = dz' \)
선전하가 있는 경우의 전계를 구하는 방법은 다음과 같으므로, \( \displaylines{\vec{E} = \frac{1}{4\pi \epsilon}\int_L \frac{\vec{r} - \vec{r}' }{|\vec{r} - \vec{r}'|^3 }\rho_l dl'\text{ } (V/m)} \) 적분하기 전의 미소전계는 다음과 같이 구할 수 있다.
\( \displaylines{ d\vec{E} = \frac{\rho_l dz'}{4\pi\epsilon_0}\frac{\rho\hat{\rho} - z'\hat{z}}{\left( \sqrt{\rho^2 + (z')^2 }\right)^3}} = dE_\rho\hat{\rho} - dE_z\hat{z} \)각 성분별로 나누어 보면
\( \displaylines{ dE_\rho = \frac{\rho_l \rho}{4\pi\epsilon_0 \left( \sqrt{\rho^2 + (z')^2 } \right)^3} dz' \\ dE_z = \frac{\rho_lz'}{4\pi\epsilon_0 \left( \sqrt{\rho^2 + (z')^2 } \right)^3 }dz' } \)
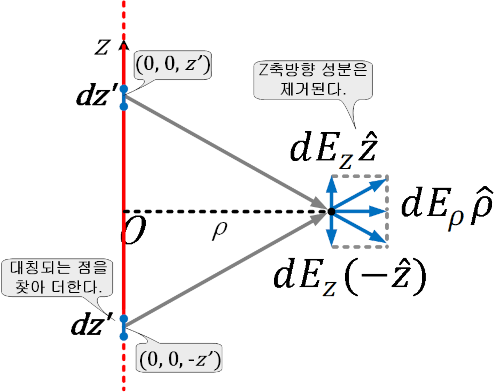
대칭성의 원리에 의해서 z축방향 성분은 모두 상쇄되므로 남는것은  ρ 축방향 성분뿐이다.

대칭성의 원리는 선전하가 고리모양으로 배열된 경우와 무한 면전하의 경우에도 동일하게 적용된다.

\( \displaylines{ \vec{E} = E_\rho\hat{\rho} = \frac{\rho_l\rho }{4\pi\epsilon_0}\int^{\infty}_{-\infty} \frac{1}{\left( \sqrt{\rho^2 + (z')^2 } \right)^3 }dz' \hat{\rho} } \)
\( \displaylines{ z' = \rho (tan \alpha) \text{ },\\\sqrt{\rho^2 +(z')^2} = \sqrt{\rho^2 + \rho^2tan^2\alpha } \\ = \rho\sqrt{1 + tan^2\alpha } = \rho\sqrt{sec^2\alpha} = \rho( sec\alpha) \\dz' = \rho(sec^2\alpha)d\alpha \text{ }, \text{ } \left\{ \begin{aligned} z' \rightarrow \infty \\ \alpha \rightarrow \frac{\pi}{2} \end{aligned}\right. \text{ }, \text{ } \left\{ \begin{aligned} z' \rightarrow -\infty \\ \alpha \rightarrow -\frac{\pi}{2} \end{aligned}\right. } \)
\( \displaylines{ E_\rho = \frac{\rho_l\rho}{4\pi\epsilon_0} \int^{\infty}_{-\infty} \frac{1}{ \left( \sqrt{\rho^2 + (z')^2} \right)^3 }dz' = \frac{\rho_l\rho}{4\pi\epsilon_0} \int^{\frac{\pi}{2}}_{-\frac{ \pi}{2}} \frac{\rho sec^2\alpha }{\rho^3sec^3\alpha } d\alpha \\ = \frac{\rho_l\rho }{4\pi\epsilon_0 }\int^{\frac{\pi}{2} }_{-\frac{\pi }{2 } } \frac{1}{\rho^2sec\alpha }d\alpha = \frac{\rho_l\rho }{4\pi\epsilon_0 }\int^{\frac{\pi}{2} }_{-\frac{\pi }{2 } } \frac{1}{\rho^2 }(cos\alpha) d\alpha \\ = \frac{\rho_l}{4\pi\epsilon_0 \rho} \left[sin\alpha \right]^{\alpha = \frac{\pi}{2}}_{\alpha = -\frac{\pi}{2}} = \frac{\rho_l }{2\pi\epsilon_0\rho } \text{ } (V/m) \\ \therefore \vec{E} = E_\rho \hat{\rho} = \frac{\rho_l }{2\pi\epsilon_0\rho } \hat{\rho} \text{ } (V/m) } \)

자유공간(ε = ε₀)에서 원통좌표계의 z=0 인 평면상에서 원점을 중심으로 반경 a[m] 인 원주상에 총 Q[C]의 전하가 균일하게 분포되어 있다고 한다.

(1) 점 (0, 0, h) 인 지점의 전계를 구하라.
(2) 전계가 최대가 되는 h 를 구하라.
(3) 만약 반경 a가 0으로 줄어들 경우 점 (0, 0, h) 인 지점의 전계를 구하라.

(1) 선전하밀도는 ρ_l  = Q/2πa (C/m) 로 균일하다. 자유공간이므로(ε = ε₀)  이다. 좌표계를 원통좌표계로 하여 계산하면 점 (0, 0, h) 상의 전계는 다음과 같다.

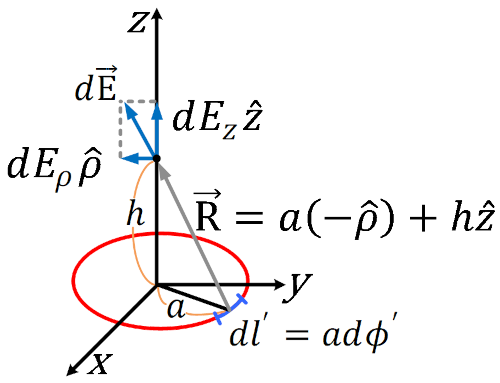
선전하가 있는 경우의 전계를 구하는 방법은 다음과 같으므로,

\( \displaylines{\vec{E} = \frac{1}{4\pi \epsilon}\int_L \frac{\vec{r} - \vec{r}' }{|\vec{r} - \vec{r}'|^3 }\rho_l dl'\text{ } (V/m)} \)
\( \displaylines{ \vec{E} = \frac{1}{4\pi\epsilon_0}\int^{2\pi}_0 \frac{Q}{2\pi a} \frac{a(-\hat{\rho}) + h\hat{z} }{\left( \sqrt{a^2 + h^2}\right)^3 }ad\phi' \\ = \left( \frac{1}{4\pi\epsilon_0}\frac{Q}{2\pi a}\right) \frac{a(-\hat{\rho}) + h\hat{z} }{\left( \sqrt{a^2 + h^2} \right)^3 }a\int^{2\pi}_0 d\phi' \\ = \frac{2 \pi Q}{8\pi^2 \epsilon_0 \left(\sqrt{a^2 + h^2} \right)^3 } \{a(-\hat{\rho}) + h\hat{z} \} \text{ }(\rho 방향 \text{ }상쇄되므로) \\ = \frac{Qh}{ 4\pi\epsilon_0 \left( \sqrt{a^2 + h^2 } \right)^3 } \hat{z} \text{ } (V/m) } \)
대칭점에 위치한 미소전하가 만든 전계를 더하면 ρ 축 방향 성분은 모두 상쇄되므로 남는 것은 z 축 방향 성분 뿐이다. 무한 선전하의 경우와 마찬가지로 여기서도 [대칭성의 원리]를 이용했다.

(2) 전계의 크기를 변수 h 대해서 미분을 취하여 0 으로 놓는다.
\( \displaylines{ \frac{|\vec{E}|}{dh} = \frac{1}{4\pi\epsilon_0} \frac{Q\left(\sqrt{a^2 + h^2} \right)^3 - Qh\frac{3}{2}(\sqrt{a^2 + h^2} )2h }{\left(a^2 + h^2 \right)^3 } \\ = \frac{1}{4\pi\epsilon_0} \frac{Q \left(\sqrt{a^2 + h^2 }\right)^3 - 3Qh^2 (\sqrt{a^2 + h^2 } ) }{ \left( a^2 + h^2 \right)^3 } \\ = \frac{1}{4\pi\epsilon_0}\frac{Q(\sqrt{a^2 + h^2}) }{\left(a^2 + h^2 \right)^3 } (a^2 + h^2 -3h^2 ) \\ = \frac{1}{4\pi\epsilon_0} \frac{Q }{\left (a^2 + h^2 \right)^{\frac{5}{2}} } (a^2 -2h^2) = 0 } \)
이 값이 0이 되게 만드는 h 의 값은 \( h = \pm \frac{a}{\sqrt{2}} \) 이다. 이 값이 전계의 크기가 최대가 되는 값이다.


(3) (1) 에서 구한 전계에서 a를 0으로 만들면 \( \vec{E} = \frac{Q}{4\pi\epsilon_0 h^2}\hat{z} \) 이 된다. 이것은 원점에 전하 Q가 있을 때의 전계와 같다.

자유공간(ε = ε₀)에서 원통좌표계의 z=0 인 무한평면상에 면전하밀도 ρ_s  가 균일하게 분포된 경우 점 (0, 0, h) 에서의 전계를 구하라.

\( \displaylines{\vec{E} = \frac{1}{4\pi \epsilon}\int_V \frac{\vec{r} - \vec{r}' }{|\vec{r} - \vec{r}'|^3 }\rho_v dv'\text{ } (V/m)} \)
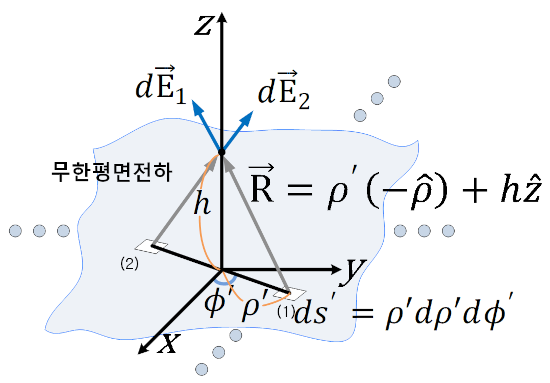
좌표계를 원통좌표계로 설정하고 미소면전하 (1)과 (2)를 설정한다. (1)과 (2)의 위치는 원점을 중심으로 대칭이다. 미소면전하 (1) 과 (2) 가 만든 전계를 점 (0, 0, h) 에서 합하면 전계는 z축 방향 성분만 남는다.  [대칭성의 원리] 때문이다. 대칭성의 원리는 무한선전하와 고리모양 선전하에서도 이용되었다.
\( \displaylines{ \vec{E} = \frac{\rho_s}{4\pi \epsilon_0 }\int^{\phi' = 2\pi}_{\phi' = 0}\int^{\rho' = \infty}_{\rho' = 0}\frac{\rho'(-\hat{\rho}) + h\hat{z}}{\left( \sqrt{(\rho')^2 + h^2 } \right)^3 }\rho'd\rho'd\phi' \\ = \frac{\rho_s }{4\pi\epsilon_0 }\int^{\phi' = 2\pi}_{\phi' = 0}\int^{\rho' = \infty}_{\rho' = 0}\frac{h\rho'\hat{z} }{\left( \sqrt{(\rho')^2 + h^2} \right)^3 }d\rho'd\phi' \\ = \frac{\rho_s}{4\pi\epsilon_0}\int^{\rho' = \infty}_{\rho' = 0}\frac{ h\rho'\hat{z}}{\left(\sqrt{(\rho')^2 + h^2} \right)^3 }d\rho'\int^{\phi' = \infty}_{\phi' = 0}d\phi' \\ = \frac{\rho_s}{4\pi\epsilon_0}\int^{\rho' = \infty}_{\rho' = 0}\frac{ h\rho'\hat{z}}{\left(\sqrt{(\rho')^2 + h^2} \right)^3 }d\rho'[\phi']^{\phi' = 2\pi}_{\phi' = 0} \\ = 2\pi \frac{\rho_s}{4\pi\epsilon_0}\int^{\rho' = \infty}_{\rho' = 0}\frac{ h\rho'\hat{z}}{\left(\sqrt{(\rho')^2 + h^2} \right)^3 }d\rho' \\ = \frac{\rho_s h}{2\epsilon_0}\int^{\rho' = \infty}_{\rho' = 0}\frac{ \rho'\hat{z}}{\left(\sqrt{(\rho')^2 + h^2} \right)^3 }d\rho' \text{ } (V/m) } \)\( (\rho' )^2 + h^2 = t \) 라 놓고 , 양변을 미분하면\( \displaylines{ 2\rho'd\rho' = dt \text{ }, \text{ } \rho'd\rho' = \frac{1}{2}dt \text{ }, \text{ } \left\{ \begin{aligned} \rho' \rightarrow \infty \\ t\rightarrow \infty \end{aligned}\right. \text{ }, \text{ } \left\{ \begin{aligned} \rho' \rightarrow 0 \\ t \rightarrow h^2 \end{aligned}\right. } \)t 로 치환하여 다시 계산하면\( \displaylines{ \vec{E} = \frac{\rho_sh}{2\epsilon_0}\int^{t=\infty}_{t=h^2} t^{-\frac{3 }{2 }}\frac{1}{2}dt\hat{z} = \frac{\rho_sh}{2\epsilon_0} \left[-t^{-\frac{1}{2} } \right]^{t=\infty}_{t=h^2}\hat{z} = \frac{\rho_s}{2\epsilon_0}\hat{z} \text{ }(V/m) } \)
z < 0 일 때에도 방향만 다를뿐, 크기는 같으므로 무한면전하가 위치한 곳 주변의 전계는 다음과 같다. 크기가 상수로 주어지므로 거리에 관계없이 , 위치에 관계없이 크기는 일정하다.\( \displaylines{ \vec{E} = \left\{ \begin{aligned} \frac{\rho_s}{2\epsilon_0}\hat{z} \text{ }, \text{ } z > 0 \\ \frac{\rho_s}{2\epsilon_0}(-\hat{z})\text{ }, \text{ } z < 0 \end{aligned}\right. \text{ }(V/m) } \)

자유공간(ε = ε₀)에서 반경이 a 인 원판이 있다. 원통좌표계의 z=0 인 원판이 놓여 있으며 중심축이 z축과 일치한다. 면전하밀도 ρ_s  가 균일하게 분포된 경우 점 (0, 0, h) 에서의 전계를 구하라.

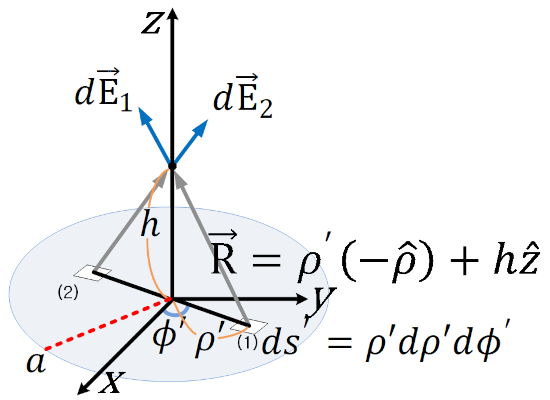
무한평면전하에서 적분범위만 a 로 바꾸면 된다.
\( \displaylines{ \vec{E} = \frac{\rho_sh}{2\epsilon_0}\int^{\rho'=a}_{\rho'=0}\frac{\rho'\hat{z}}{\left(\sqrt{(\rho')^2 + h^2} \right)^3 }d\rho' } \)
\( \displaylines{ (\rho' )^2 + h^2 = t \\ 2\rho'd\rho' = dt \text{ },\text{ }\rho'd\rho' = \frac{1}{2}dt \text{ },\text{ } \left\{ \begin{aligned} \rho' \rightarrow a \\ t \rightarrow a^2 + h^2 \end{aligned} \right. \text{ }, \text{ } \left\{ \begin{aligned} \rho' \rightarrow 0 \\ t \rightarrow h^2 \end{aligned} \right. } \)

\( \displaylines{ \vec{E} = \frac{\rho_sh}{2\epsilon_0}\int^{t=a^2+h^2}_{t=h^2}t^{-\frac{3}{2}}\frac{1}{2}dt\hat{z} = \frac{\rho_sh}{2\epsilon_0}\left[-t^{-\frac{1}{2}} \right]^{t=a^2+h^2}_{t=h^2} \hat{z} \\= \frac{\rho_s}{2\epsilon_0} \left\{1-\frac{h}{\sqrt{a^2 + h^2}} \right\} \hat{z} \text{ }(V/m) } \)

여기서 소개한 전기장을 구하는 방법은 쿨롱의 법칙을 이용하여 구하는 것이다. (상수는 가우스 법칙을 사용하여 유도되었다.) 전기장을 구하는 방법은 이 밖에도 가우스 법칙을 이용하는 방법과 포와송 방정식 또는 라플라스 방정식을 이용하는 방법이 있다. 정전계를 배우는 목적은 전기장치의 원리를 이해하는 데에 있다. 회로이론에서 배우는 R, L, C 중에서 전기장과 관련된 요소는 R, C 이다. 전자기학에서 정전계의 마지막 부분은 R, C 를 구하는 방법을 배우는 것이다. R 은 쉽게 이해할 수 있기 때문에 큰 문제가 안된다. 결국, 정전계는 커패시터에서 시작해서 커패시터로 끝난다. 커패시터를 이해할 수 있다면 정전계를 다 배운 것이다.

4. 전기장을 시각화 하는 방법

1) 전기력선 (Lines of Electric Force)
전기장은 눈에 보이지 않는다. 그렇기 때문에 이해하기가 쉽지가 않다. 전기장이 정확하게 어떻게 생겼는지는 알 수가 없다. 하지만 간단한 표시를 하면 대강의 모습을 알 수 있다. 바로 선으로 긋는 것이다. 선을 그어서 화살표를 표시해 주면 방향과 밀도를 알 수 있다. 화살표의 방향은 힘의 방향이고 선의 밀도는 힘의 크기가 된다.

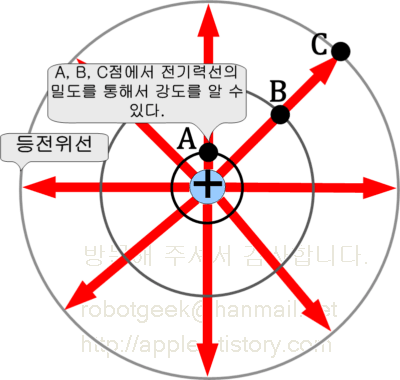
(2) 벡터(Vector)
전기력선을 사용하는 방법은 방향과 밀도를 쉽게 시각화할 수 있다는 점에서 편리하지만 크기 비교를 쉽게 하기가 어렵다. 선이 많이 때문에 시선이 분산되기 때문이다. 이럴 때는 벡터를 사용하는 것이 쉽다. 이 때는 한가지 주의할 점이 있다. 전기력선과 마찬가지로 벡터도 선과 화살표를 사용하여 표시하기 때문이다.

전기력선과 벡터를 사용하여 표시할 경우 혼란을 느끼게 되는 경우는 다음과 같은 경우이다. 평행판 커패시터에서 전기력선과 벡터를 사용해서 표시해 본다.

전기력선은 일정한 모양으로 그리게 될 것이고 벡터는 크기가 달라진다. 어떤 것이 전기력선이고 벡터인지 헷갈리기 쉽다. 점을 찍고 화살표를 그어서 그 점에서의 벡터를 표시하는 경우도 있으나, 벡터는 크기와 방향만 같으면 이동해도 같은 것으로 보기 때문에 아무 위치에 표시하는 경우도 많다. 전자기학 책을 만드는 저자 마음대로다.

유전율과 커패시터에 대한 자세한 내용은 http://appleii.tistory.com/52 참조

5. 맥스웰 방정식(Maxwell Equation)

전기장을 만드는 근원은 무엇일까? 그것은 전하(Electric Charge)이다. 음전하는 전자이며 양전하는 양성자이다. 전기장을 만드는 근원이 전하임을 수학적으로 간단히 나타낼 수 있다. 맥스웰이 이것을 깔끔하게 정리했다고 해서 맥스웰 방정식이라고 부른다. 정전계 맥스웰 방정식은 미분형과 적분형으로 나타낼 수 있으나 미분형이 좀더 깔끔하다.

정전계에서 미분형 맥스웰 2개의 뜻은 다음과 같다.

(1) 전기적 공간(Electric Field)을 변형시키는 근원은 전하(Electric Charge)이다.

그림상에서는 음전하(-)만을 표시했지만 전기적 공간(Electric Field)을 변형시키는 기(Force)를 만드는 근원은 양전하(+), 음전하(-)의 두 가지 종류가 있다는 점을 기억해 둘 필요가 있다. 왜냐하면 자기장의 N극과 S극은 따로 놀지 않고 한몸이 되어서 존재하기 때문이다. 이것이 전기와 자기의 중요한 차이점이다.


(2) 전기장은 회전하는 모양으로 표시되지 않는다.

일정한 방향을 가지는 전기장 내에서 자기 자리로 되돌아 오는 운동을 하면 전기장 내에서 한 일은 0이 된다. 다른 말로 표현하면 전기력선은 자기자신으로 돌아오는 방향으로 표시되지 않는다는 뜻이다. 

택배 배달을 하는 경우를 생각해 보자. 이경우, 택배를 배달 해야 하는 방향은 얄라딘에서 우리집으로 가는 방향으로 표시할 수 있을 것이다. 경로가 어찌되었건 얄라딘 -> 우리집 방향으로 와야 한다.

그런데 얄라딘 -> 얄라딘 으로 가는 방향으로 이동한다면 한일은 0 이 될 것이다. (택배 배달을 못 했으니 한일은 0이다.)

 
얄라딘과 우리집 사이에는 Field 가 형성되어 있다고 볼 수 있으며 이 공간의 방향을 나타낸 Vector Field 는 얄라딘 -> 우리집 방향으로 설정되어 있다고 볼 수 있다. Field 내에서 Field 의 방향과 일치하지 않는 방향으로 이동하는 것은 의미가 없다.

맥스웰 방정식(Maxwell Equation)은 많은 전자기학 책에서 다음과 같은 형태로 등장한다.

\( \nabla \times \vec{E} = 0 \)
\(\nabla \times \vec{H} = \vec{J} \)
\( \nabla \cdotp \vec{D} = \rho_v \)
\( \nabla \cdotp \vec{B} = 0 \)

외적(Cross product)은 외적끼리 내적(Inner product)은 내적끼리 '예쁘게' 모아주기 위해서 위와 같이 정리하는 것 같다. 그러나 위와 같이 놓으면 수식이 뜻하는 것이 무엇인지 명확하게 알기 어렵다. 잘못하면 '델 크로스 이는 영, 델 크로스 에이치는 제이, 델 도트 디는 로부이 ....' 식으로 암기하는 공부가 되어 버린다. 밤새도록 외워도 시험때만 되면 잊어버려서 답답했던 경험이 있는 사람이라면 뭔가 쉬운 방법을 찾게 된다. 예쁘지 않은 모양이 나와도 좀 이해하기 쉽게 하려면 순서를 바꿀 필요가 있다. 

한국조폐공사 전속모델(?)인 이황과 이이 선생에 따르면 만물의 원리는 이(理)에 있고 기(氣)의 형태로 나타난다고 한다. 구겨진 지폐 어디에도 이 사람들의 사상이 무엇인지는 나와있지 않아서 잘 모르겠지만 하여간 말은 '그럴듯하기 때문에' 살짝 인용해 보는 것도 재밌다. 그럼, 이(理)와 기(氣)에 따라서 다시 배열해 보자.

	원인(理)	현상(氣)
전기장(Electric Field)	\( \nabla \cdotp \vec{D} = \rho_v \)	\( \nabla \times \vec{E} = 0\)
자기장(Magnetic Field)	\(\nabla \times \vec{H} = \vec{J} \)	\(\nabla \cdotp \vec{B} = 0 \)

이(理)는 공간(Field)이 생기는 원인, 근원이다. 기(氣)는 관측되는 것, 느껴지는 것, 보여지는 것이다. 오른쪽의 식 2개는 공간의 모양이 어떤 식으로 생겼나를 나타내고, 왼쪽의 식 2개는 그 공간을 만들어낸 원인이 무엇인가를 나타낸다. \( \nabla \cdotp \vec{D} = \rho_v \) 는 정전계를 만드는 원인이 전하라는 뜻이고, \( \nabla \times \vec{H} = \vec{J} \) 는 정자계를 만드는 원인이 직류 전류임을 나타낸다. 원인에 의해 발생한 공간은 매질에 따라서 다르게 느껴진다. \( \nabla \times \vec{E} = 0 \) 는 전하에 의해서 발생한 것보다 약하게 느껴지며 , 발산하는 형태로 느껴진다는 뜻이다. \( \nabla \cdotp \vec{B} = 0 \) 는 직류전류에 의해서 발생한 것보다 약간 작거나 더 크게 느껴질 수 있다는 뜻이며, 발산하지 않는다는 뜻이다. 보통은 monopole 이 존재하지 않는다는 뜻으로 쓰인다. 익숙한 사람에게는 별차이가 없겠지만 처음 배우는 사람에게는 이렇게 정리하는 것만으로도 단서를 잡기가 쉬울 것이다.

6. 전기적 인력과 척력

전기장을 만드는 근원은 전하이다. 전하의 종류는 2종류이며 양극과 음극을 만든다. 같은 극끼리는 밀어내고 다른 극끼리는 잡아당긴다. 그림에서 독립된 극이 존재하는 것에 주목할 필요가 있다.

이와 비교해서 자기장은 독립된 단극(monopole) 이 존재할 수 없다. 이것이 전기장과 자기장을 분명하게 구분지어 준다. 전기장이 어느 한쪽의 극에서 나와서 다른 쪽으로 향하는 모양이라면 자기장은 자신의 위치로 돌아오는 모양을 만들기 때문이다. 장(Field)의 모양을 설명하는 것이 맥스웰 방정식에서 외적을 하는 연산이다. 외적의 모양이 0이 된다면 일정한 방향으로 향하는 모양이 될 것이고 0이 아니라면 자기 자신으로 돌아오는 모양이 된다.
자기장은 \( \nabla \cdotp \vec{B} = 0 \) 와 같이 표현된다. 자기장에서는 dipole 이 기본단위이라는 것을 나타낸 것이다. 한마디로 기본이 커플이고 싱글로서는 존재하지 않는다는 뜻이다. 우주가 생성된 초기에는 monopole 로 존재하는 자하(Magnetic Charge)가 존재했다고 하는데 현재로서는 아주 작은 확률로 존재한다고 한다.  

이해하기 어렵다면 자기야~ 는 커플이고 돌아올수 밖에 없다는 것만 기억하면 된다.



7. 장(Field)의 종류

Field 는 회전하는가 발산하는가로 따졌을 때 4종류로 나눌 수 있다.

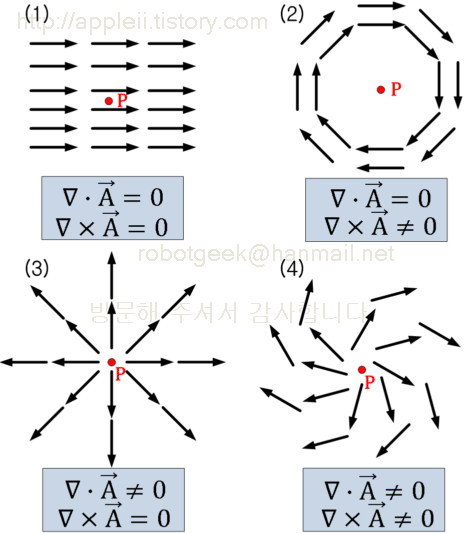
점 P를 중심으로 장의 모습을 그렸을 때 발산과 회전을 위의 그림과 같이 나타낼 수 있다. 장 벡터를 미분 연산자로 나타냈을 때 그 모양을 알 수 있다.

(1) 발산도 회전도 하지 않음
(2) 발산하지 않음. 회전함.
(3) 발산함. 회전하지 않음.
(4) 발산하면서 회전함.

장의 모양을 나타내는 표기방법을 익히는 것은 중요하다. 장의 모양은 공간이 어떤 모양으로 변형되었는가를 나타내는 것이기 때문이다. 그 공간위에 놓인 물체는 힘을 받는다. 미분연산자 두 개만으로 간단하게 어떤 방향으로 힘을 받을 것인지(또는 힘을 가하는 것인지)를 쉽게 알 수 있다.