[전자기학] 전기장에서 유전율(permittvity)의 뜻.
전기적 관점에서 물질을 나누면 도체(conductor)와 유전체(dielectric material)로 나눌 수 있다. 도체는 자유전자가 있어서 전기가 잘 통할 수 있는 물질이다. 유전체는 전기가 잘 통하지 않는 물질이다. 유전체를 배울 때 유전율(permittivity)을 배우게 된다. 유전율은 한자로 誘電率 이라고 한다. 誘電 은 전기를 유도한다는 뜻이다. 따라서 誘電率은 전기를 유도하는 정도라고 할 수 있다. 두 개의 금속판 사이에 유전율이 높은 물질을 채워넣으면 두 개의 금속판에 적은 전압을 가해도 많은 전하를 저장할 수 있다. 이것은 유전 물질의 분극(polarization) 현상 때문이다. 금속은 자유전자(free electron)가 존재하므로 전압을 가하면 일정한 방향으로 자유롭게 움직이는 것이 가능하다. 그러나 유전물질(dielectric material) 은 자유전자가 없어서 전압을 가해도 자유롭게 움직일 수 없다. 그러나 전자가 이동할 수는 없어도 한쪽으로 치우치는 형태로 변할 수는 있다. 자유전자도 없고 전기도 통하지 않아서(그래서 절연체(insulator)라고도 한다.) 아무 쓸모도 없을 것 같은 유전체가 실제로는 전기 회로에서 아주 중요한 역할을 한다. 그 원리를 알아보는 것은 재미있는 일이 될 것이다.
1. 유전체의 분극
유전체가 분극되는 경우는 다음과 같다.

1.1 극성분자 (Polar Molecules)

극성 분자(Polar Molecules)는 분자 구조상 극성을 가질 수 밖에 없는 형태다. 물(H2O)이 대표적인 극성 분자이다. 물은 산소가 음극(-)성이며 양쪽에 위치한 수소가 양극성(+)을 가지기 때문에 평소에도 분자 자체가 극성을 가지고 있다. 극성 분자는 평소에는 무질서하게 배열되어 있어서 전체적으로 봤을 때는 서로 상쇄되어 버린다. 그러나 양 극에서 전압을 가하면 일정하게 배열되어 버린다. 왼쪽 그림에서 물의 분자와 전기쌍극자가 전기적으로 같은 것으로 표시하고 있다. 앞으로는 물 분자대신 전기적으로 등가인 전기쌍극자(Electric Dipole) 형태로 표시한다.
1.2 무극성분자 (Non-Polar Molecules)
무극성 분자(Non-Polar Molecules)는 어느 한쪽으로 치우지지 않고 전기적 극성을 가지지 않는다. 그러나 양 극단에 전압을 가해주면 전자가 한쪽으로 치우치게 된다. 전자가 빠져나간 곳은 자연스럽게 양극(positive)을 가지게 된다. 이것은 양쪽으로 길게 잡아 끌어 당기는 형태가 되어 길쭉한 모양이 된다.

(2) 외부에서 전기장이 가해지면 전자가 한쪽으로 움직이며 전기적 평형상태가 깨진다.
(3) 전체적으로 보면 한쪽은 (+)극성이 강하고 다른쪽은 (-)극성이 강하다. 따라서 전기적 극성을 가지는 전기 쌍극자(electric dipole)가 된다.
물질을 이루는 원자를 전기적 관점에서 바라보면 가운데 있는 핵은 (+)전기를 가지고 있고 그 주변에 분포해 있는 전자들은 (-)전기를 가지고 있다. 원자를 구성하는 두 요소가 각각 전기를 가지고 있기 때문에 핵과 전자는 같은 극성끼리는 밀어내고 다른 극성끼리는 끌어당기는 전기적 특징을 보여주게 된다. 보통의 원자는 전자와 핵의 전기적 특성이 서로 상쇄되어서 외부에서 보면 원자 전체의 전기적 특성은 0이 되어 버린다. 그런데, 외부에서 (+)극성을 가지는 물체를 가까이 한다면 전자는 외부에서 접근하는 물체에 가까이 가려고 할 것이다. 물체를 가까이 가져가면 전자와 핵의 전기적 특성이 외부에 나타나게 된다. 전기적 중성상태의 원자를 공처럼 생겼다고 하면 이 때의 모양은 공을 찌그러트린 모양이 된다.
원자와 핵의 결합상태가 강하기 때문에 전자가 핵을 버리고 도망가는(!) 사태는 일어나기 어렵다. - 아주 강하게 쭉~ 당겨버리면 도망가는 상황이 발생하기도 한다. 이러한 현상을 유전 파괴(dielectric breakdown)이라고 한다. - 찌그러지기는 했어도 핵과의 결합은 유지해야 한다.
1.3 유전체가 분극되는 과정

(2) 외부에서 전기장을 가하면 유전체 내부에서 분극현상이 일어나서 정렬하게 되며 이웃한 서로의 극성을 상쇄시켜 버린다.
(3) 결국, 상쇄되지 않는 것은 표면 구속전하 뿐이며 표면 구속전하가 만드는 전기장이 외부에서 가한 전기장을 상쇄한다. (전기력선 4개를 상쇄)
(4) 유전체에서는 전기장이 약해진다. (전기력선 3개)
위의 그림에서 보이는 것처럼 유전체에 전기장을 가하면 분극현상이 발생한다.
위 그림을 주의해서 봐야 되는데, 실제 저런 모습으로 나타나는 것이 아니라 모두 더해서 평균을 내면 저런 모습으로 나타낼 수 있다는 것이다. 실제로는 저렇게 예쁘게(?)는 안 나온다. 일종의 상징적인 모습으로 봐야 한다. 그리고 그림으로 보면 유전체 내부의 많은 분자들 중에서 어떤 것은 분극이 되고 어떤 것은 분극이 안 되는 것처럼 보이지만 실제로는 외부 전계의 영향은 모두 받는다. 정렬되는 방향에 따라서 어떤 것은 외부 전계를 강화시키는 성분을 만들기도 하고 감소시키는 성분을 만들기도 한다. 그러나 이런 저런 성분을 다 더해서 평균내면 모두 같은 모양으로 나타낼 수 있다.
이런 문제에 대해서 Orientation Polarization 에서 잘 설명하고 있다.
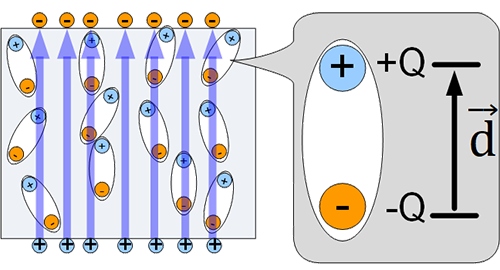
위의 그림에서와 같이 전기 쌍극자가 모두 균일하게 분포되어 있지 않다. 이럴 경우 계산하기가 까다롭기 때문에 균일하다고 가정한 새로운 도구가 필요하다. dipole moment 를 \( \vec{p} = Q \vec{d} \) (C · m) 라 하고 그것들을 모두 합하면 다음과 같다.
이것을 미소체적으로 나누면
이것을 바로 분극 벡터(polarization vector)라고 하며 단위는 C/m2 이다.
조금 더 구체적으로 들어가 보자. 분극이 일으키는 효과는 표면(surface)와 체적(volume)으로 나누어서 생각해 볼 수 있다.
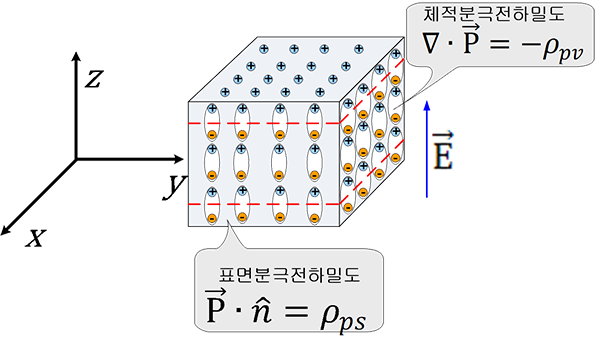
분극된 유전체의 표면에서 보았을 때 분극전하밀도(Surface density of polarization charges)는 다음과 같다.
내부에서 바라본 분극전하밀도(Volume density of polarization charges)는 다음과 같다.
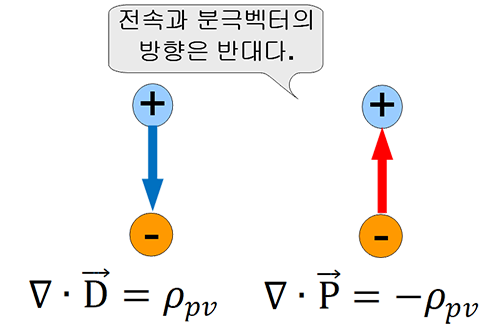
전하가 음극(negative)성으로 표시되는 것이 흥미롭다. 보통의 경우 발산의 값은 양(positive)로 표시된다. 이것은 양전하의 발산을 기준으로 하기 때문이다. 분극전하는 음전하가 발산되는 것으로 정했다는 것에 주목해 볼 필요가 있다.
균일한(homogeneous) 유전체를 가정해본다.
\( + \int\int_뒤 (-\hat{x} \cdotp \hat{z})Pdxdz + \int\int_앞 (\hat{x} \cdotp \hat{z})Pdxdz \)
\( + \int\int_{왼쪽}(-\hat{y}\cdotp \hat{z})Pdydz + \int\int_{오른쪽}(\hat{y} \cdotp \hat{z})Pdydz \)
\( = PS - PS + 0 = 0 \)
이것을 일반화 시키면 다음과 같이 표시할 수 있다. 어떠한 모양의 유전체에 대해서 총전하(Total charge)는 표면분극전하와 체적분극전하의 합이다. 그 합은 0이 된다.
= \oint_s \vec{P} \cdotp dS - \int_v \nabla \cdotp \vec{P}dv = 0 \)
결국 유전체에는 전하가 없다는 이야기인데, 이것은 유전체에는 자유전하 (free charge)가 없다는 말과 같다. 이것은 유전체에는 자유전자(free electron)가 없다고 했던 처음의 말과도 일치한다. 음전하인 전자와 양전하인 양성자는 쌍으로 존재한다. 자유전자가 없다는 것은 자유양성자가 없다는 말이다.(양성자가 맘대로 돌아다닌다는 뜻이 아니다. 전자가 떠난 빈 공간은 양성자에 의해서 양극성을 띠게 되는데 전자가 움직이면 상대적으로 양성자도 움직인 것처럼 보인다.) 이것은 자유전하가 없다는 말로 표현된다. 이것은 분극전하는 외부에서 가해진 전계에 의해서 억지로 발생한 것이기 때문이다. 즉, 분극된 상태에서 외부 전계를 차단하면 원래의 전기적 중성상태로 자연스럽게 돌아간다는 것을 뜻한다. 유전체에서 발생한 분극이란 외부의 자극에 의해서 인위적으로 발생시킨 것으로 자연스럽지 않은 현상인 것이다.
방향에 따라서 유전율이 달라지게 된다면 어떻게 될까? 방향에 따라서 일정한 것을 등방성(isotropic)이라고 하고 방향에 따라서 변하는 것을 비등방성(anisotropic, nonisotropic)이라고 한다. 그런 경우 유전율을 다음과 같이 표현한다.
전속밀도와 전계의 관계는 \( \vec{D} = \epsilon\vec{E} \) 로 표현한다. 전속밀도는 뒤에서 다룬다.
분극현상으로 분자들이 쭉 늘어서면 표면을 제외한 내부는 전하들이 가까이 위치하는데 이것은 극성을 상쇄시켜 버리므로 없는 것처럼 보인다. 따라서 남는 전하들은 표면에 위치하는 전하들뿐이다. 이 전하들이 유전체 내부에 전계를 만든다. 이 전계는 외부전계를 상쇄시키므로 외부에서 보면 전기장이 약해진 것처럼 보인다. permittivity 가 크면 분극에 의해서 내부에서 생기는 전계도 그만큼 강해진다. 여기서 주의할 것은 분극으로 나타난 전하는 어디로 이동할 수 있는 전하가 아니다. 때문에 자유롭게 이동할 수 있는 전하와 구별하기 위해서 구속전하 (bound charge)라는 말을 붙인다. 일반적으로 전하라고 하면 자유롭게 이동할 수 있는 자유전하(free charge)를 말하는 것이다.
2. 커패시터에서 유전체의 역할
더 확실하게 알려면 커패시터에서 유전체가 어떤 역할을 하는지 알아보면 된다. 커패시터는 여러 가지 모양으로 만들 수 있지만 이해하기 쉽도록 평행 도체판에 전지를 연결한 형태를 생각해 본다.

커패시터는 두 장의 금속판을 마주 보게 하고 양극판에 전극을 연결하여 두 장의 금속판 사이의 전압이 전지의 전압과 같아질 때 까지 전하를 모아주는 장치이다. 여기서 주목해야 하는 것은 전지의 전압과 양 금속판의 전압이 같아지면 그 때부터는 전하가 이동하지 않는다는 것이다. 전하를 이동시키는 것은 전지에서 가해지는 압력이며 압력이 같아지면 이동할 수 없기 때문이다. 그러므로 전하를 많이 담도록 하기 위해서는 높은 전압을 가해서 압력을 크게 하면 된다는 것을 알 수 있다.
그럼 같은 전기적 압력을 가해도 많은 전하를 가질 수 있도록 하려면 어떻게 해야 할까. 커패시터의 정전용량은 다음과 같이 표시된다.
극판의 면적과 극판의 간격은 기하학적 방법을 사용하는 것이며, 유전율은 유전체의 물리적 특성을 이용하는 것이다. 두 가지 방법을 사용하여 전하를 많이 담는 방법을 생각해 보자.
2.1 기하학적 방법
극판의 면적을 넓게 하면 담을 수 있는 전하의 개수가 늘어난다. 또 다른 방법은 두 극판의 거리를 가깝게 하는 것이다. 거리를 가깝게 하면 어떻게 될까. 우선 전위를 구하는 방법을 알아보자. 전위를 구하려면 전기장을 선적분하면 된다.
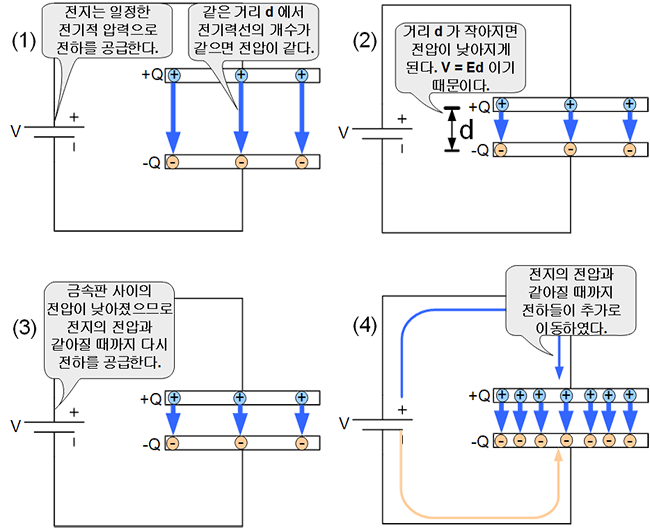
d가 작아지면 두 금속판 사이의 전압이 작아진다. 이 때 전지의 전압은 거의 일정하다. 결과적으로 두 금속판 사이의 전압이 전지의 전압보다 (일시적으로) 작아지게 된다. 따라서 전하는 이동할 수 있게 되며 두개의 금속판은 더 많은 전하를 담게 된다. 전하는 전기력을 강화시키므로 E가 커지게 된다. E가 커지면 두 금속판 사이의 전위도 커진다. 전지와 커패시터의 전위차는 점점 줄어든다. 전지의 전압과 같아질 때까지 전하는 이동한다. 결과적으로 거리 d를 줄여서 두 금속판 사이의 전압을 낮추는 효과가 있었고 이 때문에 전지와 금속판 사이의 전위차를 발생시켜서 전하가 추가로 이동할 수 있게 되는 것이다.
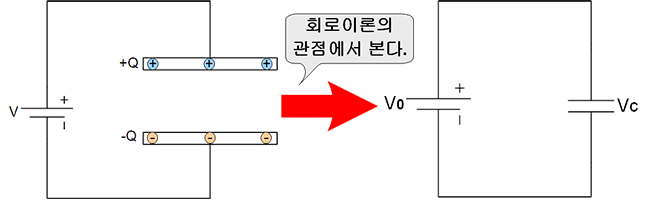
다시 말하면,
1. 초기상태는 V0 = Vc 이다. (정상상태로 전류가 흐르지 않는다.)
2. 두 극판의 간격이 줄어들면 V0 > Vc 가 된다. (회로에서 전위차 발생)
3. 전지에서 커패시터 쪽으로 전류가 흐른다. (과도상태 Transient State)
4. 커패시터의 전압이 점점 높아져서 V0 = Vc 가 되면 다시 정상상태(Steady State)가 되어 전류가 흐르지 않는다.
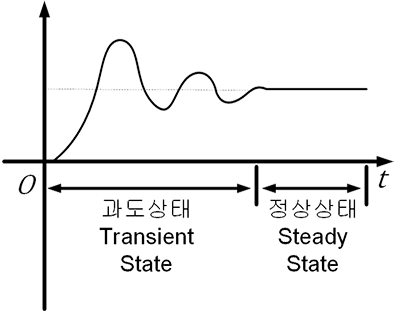
과도상태와 정상상태를 그림으로 나타내면 위와 같다. 과도상태는 값을 변화시키기 위해서 일시적으로 불안정해지는 상태이며, 정상상태는 값의 변화가 거의 없는 상태를 말한다.
그럼 가해지는 전압을 낮추어주는 또 다른 방법은 무엇인가.
2.2 유전체를 이용하는 방법
유전물질은 외부에서 가해진 전기장을 약화시킨다. V=Ed에서 E를 작게 만드는 것이다. E가 작아지면 V가 작아지고 압력 차이에 의해서 전하가 추가로 이동할 수 있게 된다. 이러한 이동은 양 극판의 전압이 전지의 전압과 같아질 때까지 계속된다. 따라서 유전물질을 금속판 사이에 끼워주면 전하를 금속판에 더 많이 담을 수 있게 된다.

위 그림은 유전체를 금속판 사이에 끼운 커패시터에 전지를 연결하여 전하를 공급했을 때 발생하는 상황을 나타낸 것이다. 전하를 공급할수록 전계가 강해지므로 내부에서 분극이 잘 일어나서 전하로부터 나오는 전계를 상쇄시켜 버린다. 그러나 무한정 상쇄시켜 버리지는 못하므로 외부에 나타나는 전계가 있게 된다. 이것이 금속판 사이의 전위차를 만들어서 전압을 점점 높여준다. 전지의 전압과 같아지면 전하의 공급은 중단된다. 유전체가 있으면 금속판에 저장되는 전하가 더 많아지는 것을 알 수 있다. 오른쪽 아래 그림은 유전체가 없을 때의 그림이다. 유전체와 관계없이 두 극판 사이의 전기력선 개수는 일정하다. 이것은 전압과 관계있기 때문이다.
2.3 전하충전 후 유전체를 뺐을 때의 전압변화
그렇다면 한 가지 의문점이 생긴다. 충전이 완전히 이루어진 다음 전지와의 연결을 끊는다. 그리고 그 상태에서 유전물질을 빼면 어떻게 될까? 전하들이 이동할 통로를 없애버렸으니 금속판에 있는 전하들은 그대로이다. 그리고 유전물질이 없어졌으므로 상쇄시킬 전기력이 없다. 따라서 전하에 의해 발생하는 전기력선이 외부에 노출된다. 이것은 결과적으로 전기력선 밀도를 높여주므로 전위차가 커지는 효과가 있다. 원래의 전지전압보다 더 커지는 것이다.

2.4 전하충전 후 유전체를 넣었을 때의 전압변화
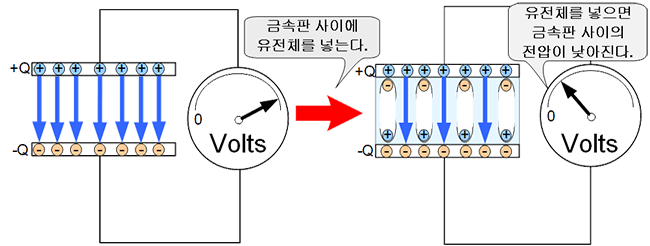
반대의 상황을 생각해 보자. 전하가 충전된 두 금속판 사이에 유전물질을 채워 보자. 그럼 분극 현상이 발생하고 내부에서 발생한 전계가 상쇄시킬 것이다. 유전물질을 채운 뒤에 전압을 측정해 보면 전압이 낮아지게 된다.
3. 전속밀도와 전계의 관계
그럼 이제, \( \vec{D} \) 와 \( \vec{E} \) 의 관계에 대해서 생각해 볼 필요가 있다. wikipedia 에 아주 중요한 내용이 있다.
D 와 E 는 대전된 물체에 대해 작용하는 같은 현상을 나타내는 것이다. D는 이 작용에서 전하 밀도와 관련된 것이고 , E는 힘과 전위차에 관련된 것이다.
>>전하량 또는 전하의 개수가 같다면 D는 같을 것이고 , 전압이 같다면 E가 같을 것이다.
전계에 관한 내용은 https://appleii.tistory.com/74 참조
전속밀도(D)와 전계강도(E)에 대한 내용은 https://appleii.tistory.com/113 참조
3.1 전속밀도의 정의

유전체 외부의 전하에 의한 전기력선 \( \vec{D} \) 는 유전체를 통과하면서, 일부는 유전체의 분극을 만드는데 사용되었고 ( \( \vec{P} \) ) 나머지는 유전체를 통과했다( \( \epsilon_0 \vec{E} \) ). 자유 공간(free space)이라면 모두 통과하였을 것이다. 가해준 전기력선을 감소시키므로 손해를 보는 느낌이 든다. 하지만 꼭 그런것만은 아니다. 분극을 일으키게 되면 유전체 표면에 구속 전하(bound charge) 가 생기기 때문이다. 구속 전하는 평행 도체판을 이용하여 커패시터를 만들때 도체판에 전하를 끌어당기는(유도하는) 중요한 역할을 한다.
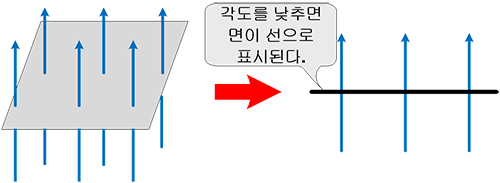
그럼 벡터로 표시하면 어떻게 될까?
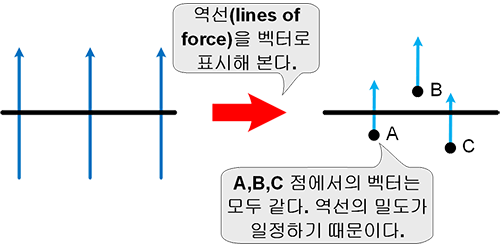
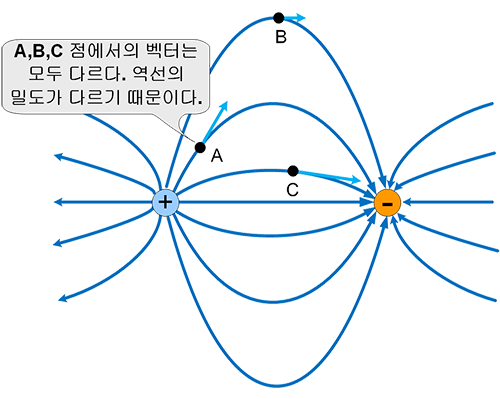
커패시터를 다시 생각해 보자. 두 도체 사이에 유전체가 있다. 알고 싶은 것은 도체 사이의 유전체를 통과하는 역선이다. 그러므로 면을 두 도체 사이에 위치시켜야 할 것이다.
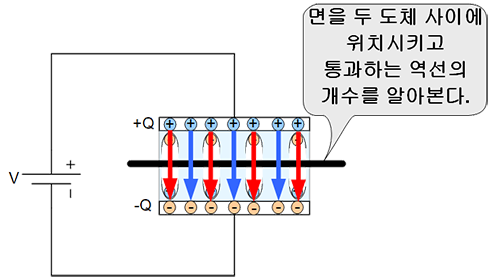
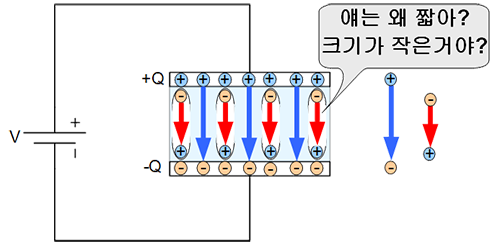
오해를 피하기 위해서 다시 한번 그림을 보자. 그림은 실제보다 과장되게 그려진 것이다. 금속판과 유전체가 맡닿는 경계면은 아주 얇다. 파란색 화살표인 전기력선은 금속판의 양전하로부터 나온다. 빨간색 화살표인 분극선은 유전체의 음전하로부터 나온다. 이것을 벡터로 오해해서 길이에 따라서 크기가 다른 것처럼 보이는 것을 피하기 위해서 같은 길이로 그렸다. 정확하게 그리자면 다음과 같이 그려야 한다.
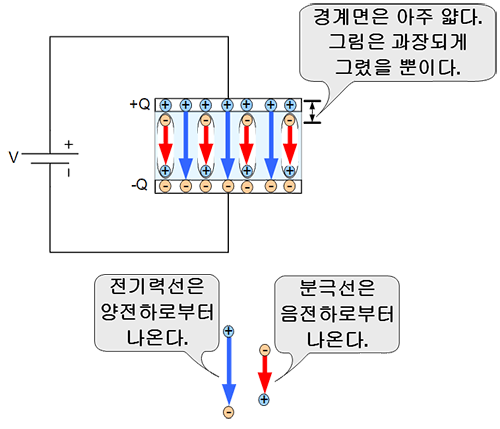
\( \vec{E}\) 와 \(\epsilon_0 \vec{E} \) 의 관계는 무엇일까? 그것은 기준이 되는 것이 점이냐 면이냐 하는 것이다. \( \vec{E} \) 는 기준이 점이고 \(\epsilon_0 \vec{E} \) 는 기준이 되는 것이 면이다. 전계강도 \( \vec{E} \)는 전계가 있는 한 지점에서의 가상전하 +1C 이 느끼는 전계의 세기이며 전기력선의 밀도인 \(\epsilon_0 \vec{E} \) 는 단위면적( 1 m2 ) 을 통과하는 전기력선의 개수이다. 둘 다 동일한 것을 나타내고 있지만 면을 사용할 경우 가우스 법칙(Gauss's Law)을 사용하면 계산이 간단해 진다는 장점이 있다.
전지로부터 평행 도체판에 전하를 이동시키기 위해서는 전위차가 유지되어야 한다. 도체판 사이의 전위차를 만드는 것은 \(\epsilon_0 \vec{E} \) (전기력선 3개)이다. 전지의 입장에서 보면 두 도체판 사이의 전위차는 유전물질이 있거나 없거나 상관이 없이 모두 같다(전기력선 3개). 왜 그런지 다음 그림을 보자.

(2) 그림에서 그 부분을 지운다.
(3) 모두 지워본다.
(4) 최종적으로 전지가 느끼는 커패시터의 모습이다.
결론은 이렇다. 일정한 전압을 가했을 때 유전체에서 분극이 발생한다. 이 분극은 외부에서 가해진 전기장과 반대방향의 전기장을 형성하므로 외부 전기장을 상쇄시켜 보이지 않도록 만든다. 그러나 중요한 것은 전기장이 외부에 보이지 않을 뿐 전하는 그대로 잡아둔다는 점이다. 즉, 유전체의 존재 때문에 더 많은 전하를 붙들어 둘 수 있는 것이다. 바로 이러한 점 때문에 유전체를 커패시터에서 사용하는 것이다. 커패시터는 전하를 붙잡아 두는 장치이고 유전체가 있으면 더 많이 붙잡아 둘 수 있기 때문이다. 이제는 유전율(誘電率)의 뜻을 알 수 있다. 전기를 유도(誘電) 한다는 뜻이 무엇인지 분명히 알 수 있게 되었다. 영어로는 permittivity 라고 하는데, 그 정확한 의미에 대해서는 여러가지가 있는 것 같다. 하지만 유전율(誘電率)의 뜻을 생각하면서 permittivity 를 해석해 보면 유전체와 닿은 도체에 전하가 오도록 허용(permit)한다는 뜻으로 해석하는 것이 자연스러울 것 같다. 유전율의 단위는 F/m 이다. 정전용량을 뜻하는 F(Farad)가 있는 것을 알 수 있다. 유전율이 높으면 많은 전하를 끌어 모을 수 있으므로 정전용량이 커진다.
3.2 분극벡터의 정의
분극 벡터 \( \vec{P} \) 는 위와 같이 나타낼 수 있다. 방향을 (-) 에서 (+) 로 정해버렸기 때문에 \( \vec{E} \) 방향과 같다. 위 정의를 다시 쓰면 \( \vec{P} = k\vec{E} \) 와 같이 된다. 이것은 \( \vec{P} \) 와 \( \vec{E} \) 의 관계가 선형(linear)이라는 것을 나타낸다. 선형이 있다면 비선형(nonlinear)관계도 있을 것이다. 그러나 대부분의 유전체가 선형이므로 비선형은 일단 생각하지 않도록 한다. 또한 모든 유전체는 \( \chi_e \) > 0 이며 진공(vacuum)에서 \( \chi_e \) = 0 이다.
전속밀도 \(\vec{D}\) 는 최종적으로 위와 같이 정리된다. \( \epsilon_r \)은 차원이 없는(dimensionless) 그냥 상수이다. 자유공간(free space)에서의 유전율 \( \epsilon_0\) 와 비교하여 상대적인 값을 따지므로 상대 유전율(relative permittivity) 또는 유전상수(dielectric constant)라고 한다. \( \chi_e \) 는 분극이 잘되는 정도를 나타낸 것으로 전화율(electric susceptibility)이라고 하며 역시 상수이다.
1. He’s highly susceptible to flattery. (그는 아부에 약하다.)
2. Some people are more susceptible to alcohol than others. (어떤 사람들은 다른 사람들보다 알코올에 더 영향을 받기 쉽다.)
외부의 영향, 자극에 대해서 민감하게 반응한다는 느낌으로 susceptibility 를 이해하면 된다.
\( \chi_e \) = 5 라면 분극되는 정도가 유전체 내부 전기장의 5배라는 이야기가 된다. 내부 전기장을 1로 생각한 값이므로 \( \epsilon_r\) 이 8이면 분극되는 정도인 \(\chi_e \)는 7이라는 것을 쉽게 알 수 있다.
몇가지 물질의 유전상수를 나타내 보면 다음과 같다.
| Material | Dielectric Constant | Dielectric Strength (V/m) |
| Water(Sea) | 80 | |
| Paper | 7 | 12 x 106 |
| Glass | 5 ~ 7 | 35 x 106 |
| Mica | 6 | 70 x 106 |
| Paraffin | 2.2 | 30 x 106 |
| Air (1 atm) | 1 | 3 x 106 |
\( \chi_e \) 는 1보다 클수도 있고 작을수도 있다. [그림 3.1]에서 벡터D 가 5이고 내부에서 보이는 전기장이 3, 분극이 2가 되는 비율이라면 상대유전율은 1.66, 내부전기장은 1, 전화율은 0.66이 된다. 이런 경우라면 내부전기장보다 분극의 세기가 작을 것이다.
3.3 전속밀도를 도입한 이유
그럼, 왜 전계 \( \vec{E} \) 만으로 설명하지 않고 전속밀도 \( \vec{D} \) 를 추가로 도입하였을까? 앞에서 본 것처럼 유전체에서는 내부 분극 현상 때문에 가해진 전계를 약화시킨다. 이것은 매질에 따라서 내부 전계가 다르다는 이야기가 된다. 따라서 전기적 관점을 전계만으로 설명하면 매우 복잡해진다. 외부에서 가해진 전계, 내부에서 분극 때문에 생기는 전계, 분극 때문에 약해진 전계 ... 이런식이면 설명도 길어지고 이해하기 어려워진다. 때문에, 외부에서 매질에 가해지는 영향력을 \( \vec{D}\) (유전체 외부의 전하로부터 발생)라고 분명하게 표시하고 이것이 매질내에서 어떻게 나타나는 가를 \( \epsilon_0\vec{E}\) 와 \(\vec{P}\) 로 나타내는 것이다. \( \vec{P} \) 를 다시 정의하여 \( \vec{D}\) 를 다시 정리하면 \( \vec{D} = \epsilon\vec{E} \) 라는 단순한 모양으로 나타낼 수 있다. 어떻게 보면 수식을 이리저리 가지고 놀아본 '수식장난'인 셈인데 배우는 입장에서는 왜 만들었는지 알 수가 없어서 꽤나 답답하다.
전계 \( \vec{E} \) 는 단위가 N/C 이다. 단위 양전하가 느끼는 전계의 강도를 뜻한다. 전속밀도 \(\vec{D} \) 는 단위가 C/m 2 이다. 단위 면적을 통과하는 전기력선을 뜻한다. \( \vec{E}\) 는 매질에 따라 변하는 값이지만, \(\vec{D} \) 는 매질과는 무관하게 전계를 만들어낸 원래의 전하(Free Charge)가 만들어낸 값이다.
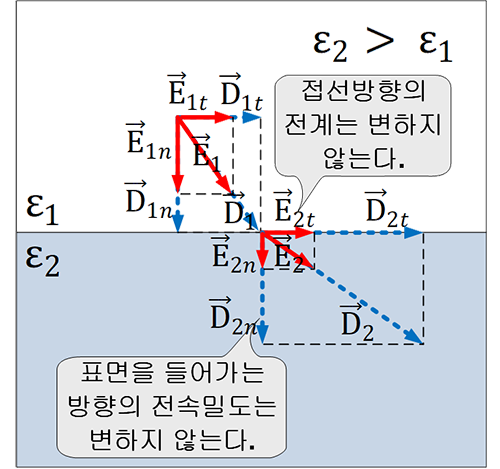
다시 말하자면 , 전속밀도가 매질에 따라서 변하지 않는다는 말은 \( \vec{D}_{1n} = \vec{D}_{2n} \) 이라는 뜻이다. 그러므로 매질이 달라지면 \( \vec{D}_1 \ne \vec{D}_2\) 가 된다.
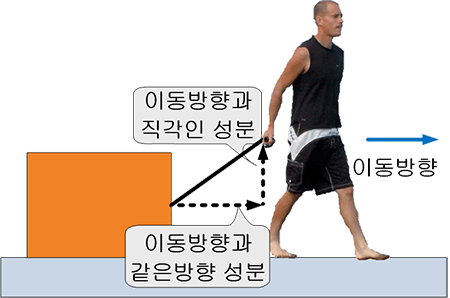
물리학의 역학 부분에서 비스듬하게 물체를 끌고 갈때, 이동방향과 같은 성분에만 관심을 가지는 것과 같다. 이동방향과 다른 방향은 신경쓸 필요가 없다.
4. 문제풀이
개념을 확인하는 의미에서 간단한 문제를 풀어보자.
(a) D
(b) P
(c) 도체판 표면의 자유전자의 전하밀도 (The surface charge density of free charge on the plates)
(d) 분극된 전하의 표면 전하밀도 (The surface density of polarization charge)
(e) 두 도체판 사이의 전위차 (The potential difference between the plates)
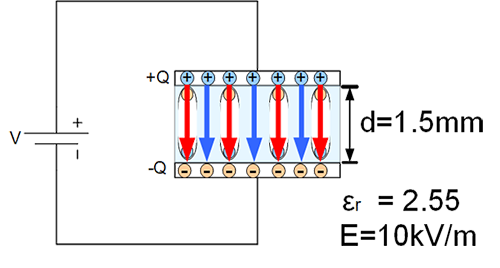
\( (a) \text{ } D = \epsilon_0 \epsilon_r E = \frac{10^{-9}}{36\pi}(2.55)10^4 = 225.4 (nc/m^2) \)
\( (b) \text{ } P = \chi_e \epsilon_0 E = (1.55)\frac{10^{-9}}{36\pi}10^4 = 137 (nc/m^2) \)
\( (c) \text{ } \rho_s = \vec{D} \cdotp \hat{n} = D_n = 225.4 (nC/m^2) \)
\( (d) \text{ } \rho_{\rho s} = \vec{P} \cdotp \hat{n} = P_n = 137 (nC/m^2) \)
\( (e) \text{ } V = Ed = 10^4(1.55 \cdotp 10^{-3}) = 15 (V) \)
(a) , (b) 에서 D, P 는 스칼라량으로 전하밀도(C/m2)만을 구하는 것이다. 벡터( \(\vec{D} \) , \(\vec{P} \) )가 아니라는 것을 주의해야 한다.
(c) , (d) 의 결과는 (a) , (b) 와 같다. 개념을 이해했다면 당연한 결과이다. 전기력선은 자유전하(free charge)로부터 나오는 것이다. 또한 이것은 도체표면으로부터 나온것이므로 표면전하밀도 (c) 와 전속밀도 (a) 는 같다. 분극이 일어나면 내부에서는 서로 극성을 상쇄시키므로 결국 남는것은 표면에 위치한 전하뿐이다. 따라서, 표면에 위치한 분극 전하밀도(d) 는 (b) 와 같다. \(\epsilon_r\) = 2.55 이므로 \( \epsilon_0\vec{E} \) 가 1 일 때 \(\vec{P} \) 는 1.55 임을 알 수 있다. (위 그림에서 파란색 화살표보다 빨간색 화살표가 더 많다. )
(a) 전화율 \( \chi_e \)
(b) 전계 \(\vec{E} \)
(c) 상대유전상수 \(\epsilon_r \)
(d) 전속밀도 \(\vec{D} \)
(a) \( \vec{P} = \chi_e\epsilon_0\vec{E} = 2\cdotp \frac{10^{-9}}{36\pi} (3\hat{x} - 4\hat{y} + 2\hat{z}) \) (C/m2)
(b) \( \vec{E} = 3\hat{x} - 4\hat{y} + 2\hat{z} \) (N/C)
(c) \( \epsilon_r = (1 + \chi_e) = 3 \)
(d) \( \vec{D} = \epsilon\vec{E} = \epsilon_r\epsilon_0\vec{E} = 3\epsilon_0\vec{E} = \frac{10^{-9}}{36\pi} (9\hat{x} - 12\hat{y} + 6\hat{z}) = \frac{1}{36\pi} (9\hat{x} - 12\hat{y} + 6\hat{z}) \) (nC/m2)
자유공간의 유전율 \( \epsilon_0 = \frac{10^{-9}}{36\pi} \) (F/m) 의 값과 \( \vec{P} \) 가 어떻게 표현되는지 안다면 금방 풀 수 있는 문제다. 약간의 트릭을 사용하여 n(nano) 를 10-9 으로 바꾸고 괄호 안에서 2를 밖으로 빼내면 \( \vec{P} \) 의 표현식으로 바뀐다. \( \chi_e \) = 2 라는 것을 쉽게 알 수 있다.
\( \left[ \begin{matrix} D_x \\ D_y \\ D_z \end{matrix} \right] = \epsilon_0 \left[ \begin{matrix} 4 & 1 & 1\\ 1 & 4 & 1\\ 1 & 1 & 4 \end{matrix} \right] \left[ \begin{matrix} E_x \\ E_y \\ E_z \end{matrix} \right] \)
\( \vec{E} = 10\hat{x} + 20\hat{y} -30\hat{z} \) (V/m) 라고 할 때, \( \vec{D}\) 를 구하라.
\( \left[ \begin{matrix} D_x \\ D_y \\ D_z \end{matrix} \right] = \epsilon_0 \left[ \begin{matrix} 4 & 1 & 1\\ 1 & 4 & 1\\ 1 & 1 & 4 \end{matrix} \right] \left[ \begin{matrix} \phantom{-} 10 \\ \phantom{-} 20 \\ -30 \end{matrix} \right] = \epsilon_0 \left[ \begin{matrix} \phantom{-} 30 \\ \phantom{-}60 \\ -90 \end{matrix} \right] = \frac{10^{-9}}{36\pi} \left[ \begin{matrix} \phantom{-} 30 \\ \phantom{-} 60 \\ -90 \end{matrix} \right] \)
\(\vec{D} \) 의 스칼라 성분들이 위와 같으므로 다음과 같이 쓸 수 있다. \( \vec{D} = 0.2653\hat{x} + 0.5305\hat{y} - 0.7958\hat{z} \) (nC/m2)
(1) 표면분극전하밀도, 체적분극전하밀도를 구하라.
(2) 구속전하의 총합은 0임을 증명하라.

(1) 표면분극전하밀도는 x방향일때 \( \rho_{ps} = \vec{P}\cdotp\hat{x} = P_0(x\hat{x} + y\hat{y} + z\hat{z})\cdotp\hat{x} = P_0x(\hat{x}\cdotp\hat{x}) = P_0x \) 이고, x=L/2 일 때
\( [P_0x]_{x=\frac{L}{2}} = P_0\frac{L}{2} \) 이다.
체적분극전하밀도는
\( \rho_{\rho v} = -\nabla \cdotp \vec{P} = - ( \frac{\partial} {\partial x}\hat{x} + \frac{\partial }{\partial y}\hat{y} + \frac{\partial}{\partial z}\hat{z} )\cdotp P_0 (x\hat{x} + y\hat{y} + z\hat{z} ) \)
\( = - P_0\{ \frac{\partial x }{\partial x} (\hat{x} \cdotp \hat{x}) + \frac{\partial y }{\partial y} (\hat{y} \cdotp \hat{y}) + \frac{\partial z }{\partial z} (\hat{z} \cdotp \hat{z}) \} \)
\( = -P_0(1 + 1 +1) = -3P_0 \) 이다.
(2) 표면전하는
\( Q_s = \oint_S \rho_{\rho_S}dS = 6\int^{\frac{L}{2}}_{- \frac{L}{2}}\int^{\frac{L}{2}}_{- \frac{L}{2}} P_0\frac{L}{2}dydz \)
\( = 6\cdotp P_0 \frac{L}{2} \int^{\frac{L}{2}}_{- \frac{L}{2}}dy\int^{\frac{L}{2}}_{- \frac{L}{2}}dz = 3P_0L[y]^{y=\frac{L}{2}}_{y=-\frac{L}{2}} [z]^{z=\frac{L}{2}}_{z=-\frac{L}{2}} \)
\( = 3P_0L \cdotp L \cdotp L = 3P_0L^3 \)
체적전하는
\( Q_v = \oint_v \rho_{\rho_v}dv = \int^{\frac{L}{2}}_{- \frac{L}{2}}\int^{\frac{L}{2}}_{- \frac{L}{2}} \int^{\frac{L}{2}}_{- \frac{L}{2}} (-3P_0)dxdydz \)
\( = -3P_0 \int^{\frac{L}{2}}_{- \frac{L}{2}}\int^{\frac{L}{2}}_{- \frac{L}{2}} \int^{\frac{L}{2}}_{- \frac{L}{2}} dxdydz = -3P_0\int^{\frac{L}{2}}_{- \frac{L}{2}}dx\int^{\frac{L}{2}}_{- \frac{L}{2}}dy \int^{\frac{L}{2}}_{- \frac{L}{2}} dz\)
\( -3P_0[x]^{x=\frac{L}{2}}_{x=-\frac{L}{2}} [y]^{y=\frac{L}{2}}_{y=-\frac{L}{2}} [z]^{z=\frac{L}{2}}_{z=-\frac{L}{2}}\) \( =-3P_0 \cdotp L \cdotp L \cdotp L = -3P_0L^3 \)
둘을 합하면
\(Q_t = Q_s + Q_v = 3P_0L^3 - 3P_0L^3 = 0 \) 이다. 따라서 구속전하의 총합은 0이다.
(1) 표면분극전하밀도와 체적분극전하밀도를 구하라.
(2) 구속전하의 총합은 0임을 증명하라.
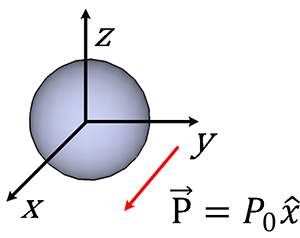
(1) 표면분극전하밀도는
\( \rho_{\rho s} = \vec{P}\cdotp \hat{r} = P_0(\hat{x}\cdotp \hat{r}) = P_0sin\theta cos\theta \)
체적분극전하밀도는
\( \rho_{\rho v} = -\nabla \cdotp \vec{P} = - ( \frac{\partial} {\partial x}\hat{x} + \frac{\partial }{\partial y}\hat{y} + \frac{\partial}{\partial z}\hat{z} )\cdotp P_0 \hat{x} \)
\( = - \{ \frac{\partial P_0}{\partial x} (\hat{x} \cdotp \hat{x}) \} = 0 \) 이다.
(2) 표면전하는
\( Q_s = \oint_s \rho_{\rho s}dS = \int^{\pi}_0 \int^{2\pi}_0 P_0b^2 sin^2\theta cos\phi d\phi d\theta \)
\(= P_0 b^2 \int^{2\pi}_{0} cos\phi d\phi \int^{\pi}_{0}sin^2\theta d\theta \)
\( = P_0 b^2 \int^{2\pi}_{0}cos\phi d\phi \int^{\pi}_{0} \frac{1-cos2\theta}{2} d\theta \)
\( = P_0b^2[sin\phi]^{2\pi}_{0} [\frac{1}{2} \theta - \frac{sin2\theta}{4}]^{\pi}_{0} = P_0 \cdotp 0 \cdotp (\frac{\pi}{2}) = 0 \)
체적전하는
\( Q_v = \int_v \rho_{\rho v}dv =0 \)
구속전하의 총합은
\( Q_t = Q_s + Q_v =0 \)
이다. 균질한(homogenous)한 매질에서 유전체의 모양이 어떠하든 구속전하의 총합은 0 이다.
(1) 표면분극전하밀도와 체적분극전하밀도를 구하라.
(2) 구속전하의 총합은 0임을 증명하라.

체적분극전하밀도는
\( \rho_{pv} = -\nabla \cdotp \vec{P} = - ( \frac{\partial}{\partial x} \hat{x} + \frac{\partial}{\partial y}\hat{y} + \frac{\partial}{\partial z}\hat{z} ) \cdotp P_0 (3x\hat{x} + 4y\hat{y} ) \)
\( = -P_0 \{ \frac{\partial (3x)}{\partial x} (\hat{x} \cdotp \hat{x}) + \frac{\partial (4y)}{\partial y} (\hat{y} \cdotp \hat{y}) \} = -P_0 (3 + 4) \)
\( = -7P_0 \)
체적전하는
\( Q_v = -7P_0 \pi ({\rho_o}^2 - {\rho_i}^2) \)
표면분극전하밀도는 안쪽면과 바깥쪽 면으로 나누어서 계산한다.
바깥쪽 면은
( \( \rho = \rho_0 , \hat{n} = \hat{\rho} \) )일때
\( \rho_{\rho so} = \vec{P} \cdotp \hat{\rho} = P_0(3 \rho_0 cos \phi \hat{x} + 4 \rho_0 sin \phi \hat{y})\cdotp \hat\rho \)
\( = P_0 \rho_0 \{ {3cos \phi (\hat{x} \cdotp \hat{\rho}) + 4 sin \phi (\hat{y} \cdotp \hat{\rho}}) \} \)
\( = P_0 \rho_0 (3cos^2 \phi + 4sin^2 \phi) \)
\( = P_0 \rho_0 \{ 3(cos^2 \phi + sin^2 \phi ) + sin^2 \phi \} \)
\( = P_0 \rho_0 (3 + sin^2 \phi) \)
안쪽 면은
( \( \rho = \rho_i \text{ } , \text{ } \hat{n} = -\hat{\rho} \) ) 일때
\( \rho_{\rho si} = \vec{P} \cdotp (-\hat{\rho}) = -P_0 \rho_i (3 + sin^2 \phi) \) 이다.
표면전하는 바깥쪽은
\( Q_{so} = \int_s \rho_{\rho so}dS = \int^{2 \pi}_{0} \rho_{\rho so} \rho_0 d\phi = \int^{2\pi}_{0}P_0 \rho_0 (3 + sin^2\phi)\rho_0 d\phi \)
\( = P_0 {\rho_0} ^2 \int^{2\pi}_{0} (3 + sin^2 \phi) d \phi \)
\( = P_0 {\rho_0}^2 \int^{2\pi}_{0} (3 + \frac{1 - cos2\phi}{2}) d\phi \)
\( = P_0 {\rho_0}^2 \int^{2\pi}_{0} (3 + \frac{1}{2} - \frac{cos2\phi } {2}) d\phi \)
\( = P_0 {\rho_0}^2 [\frac{7}{2}\phi - \frac{sin2\phi}{4} ]^{\phi = 2\pi }_{\phi = 0} = 7\pi P_0 {\rho_0}^2 \)
안쪽은
\( Q_{si} = -7\pi P_0 {\rho_0}^2 \)
구속전하의 총합은 \( Q_t = Q_{so} + Q_{si} + Q_v = 0 \) 이다.
따라서 구속전하의 총합은 0이다.